真空管道流導計算中平均壓力取值的誤差分析與計算方法
真空管道的流導,又叫做通導能力。它是管道的重要性能參數,是設計真空系統時必須考慮的因素之一。在計算粘滯流管道流導時,流導跟管道內的平均壓力有關,通常的方法是近似把管道入口壓力作為管道平均壓力。但是當管道較長、真空泵抽速較低或管道入口壓力較小時,上述近似方法的誤差就變大了。本文對粘滯流下管道的平均壓力的取值進行了討論,分析了近似取管道高壓端壓力為平均壓力時所產生的誤差,并提供了粘滯流下管道的平均壓力的計算方法等。
1、目前真空管道粘滯流態流導計算中的問題
在粘滯流態下的管道流導與真空管道內的平均壓力p 有關。通常管道的平均壓力取為:

式中:p1 為抽氣管道的進口壓力,p2 為抽氣管道的出口壓力,即真空泵的入口壓力。在真空系統設計中,通常僅是知道真空室內的壓力,即抽氣管道入口處的壓力,因此在計算抽氣管道的平均壓力時,一般都是近似把抽氣管道入口處的壓力作為管道的平均壓力。其理論根據是,在真空系統抽氣過程中,僅是在粗抽階段存在粘滯流,而粗抽管路的流導C 一般都比較大。根據真空技術基本方程,在泵的抽速Sp 較低、管道流導C 較大的情況下,真空泵對真空室的有效抽速Se 近似等于真空泵在入口壓力下的抽速Sp, 即若C垌Sp時, 則Se≈Sp。則根據氣體連續性方程可得:Q=p1Se=p2Se,所以p1≈p2,從而得到p=p1。但是,這僅是在假設粗抽泵的抽速相對于抽氣管道的流導來說很小時,這樣的近似取值方法才存在一定的合理性。但是在粘滯流下管道的流導與平均壓力成正比,隨著真空泵的不斷抽氣,管道的流導逐漸下降,當泵的抽速與管道的流導相差不大時,就會存在較大的偏差。下面我們對平均壓力近似取值為抽氣管道入口端壓力時的誤差進行定性地分析。當管道為長管時,把式(1)代入流導定義式可得粘滯流圓截面管道流導為
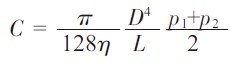
假設真空泵的抽速Sp 不變,則Q=P2Sp,根據管道流導的定義得
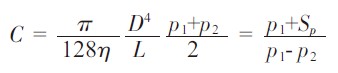
解得:

注意,上面兩式中Sp 實際上是對應泵入口壓力p2 下的抽速,在Sp 未知的情況下,僅在抽速Sp 為常數的壓力范圍內有解。當抽速隨著真空泵入口壓力變化時,因Sp 是隨著p2 變化的,而p2 未知,所以無法確定抽速Sp,從而無法計算管道的平均壓力。
2、真空管道平均壓力的誤差分析與計算方法
由上所述,在真空管道粘滯流態的流導計算中,當真空泵的抽速發生變化時,需要對真空泵的抽速曲線進行數值化擬合,建立p2 與Sp 之間的函數關系,從而可以根據p2 與Sp 之間的關系和上述公式進行聯立方程組解算出管道出口壓力p2,即可計算出管道的平均壓力p,從而進一步準確計算管道的流導。
例如,假設真空泵連接真空室的管道D=0.04 m,L=1 m,真空泵的抽速為8 L/s,氣體為20℃的空氣。若管道入口處壓力,假設真空泵抽速S 不變,此時由于L/D>20,管道為長管,則由式(2)得:

若近似把抽氣管道入口壓力近似取為管道的平均壓力,即p=p1=100 Pa。從以上計算可以知道,在這個算例中,當系統壓力(管道入口壓力)較高時,這兩種管道平均壓力確定方法的取值偏差很小,相對誤差僅約為1.2%。但是當管道入口壓力較低時,兩者取值偏差就會很大。例如,真空系統條件同前(D=0.04 m,L=1 m,S=8 L/s),使用該泵從大氣壓抽到10 Pa時,其平均壓力的取值相對誤差隨著管道入口壓力的變化曲線如圖1 所示,由圖可以看出,若是管道入口壓力很高時,此時管道的流導也很大,管道的平均壓力p 近似取入口壓力p1,相對誤差很小,隨著入口壓力的降低,管道的流導也降低,相對誤差也會增大,此時近似把管道入口壓力取值為平均壓力就不適用了。由圖可以看出,隨著管道入口壓力的下降,相對誤差逐漸增大,最大相對誤差達到了11.5%。
對于短管道:當D=0.04 m,L=0.5 m,S=8 L/s時,使用同一臺真空泵從大氣壓抽到10Pa 時,由于L/D>20,管道為短管,假設真空泵抽速為常數,使用式(3)計算p2,其相對誤差隨著導管入口壓力的變化曲線如圖2 所示。誤差趨勢和長管時的誤差趨勢一樣,最大誤差達到了5.7 %。由圖1 和圖2 可以看出,即使當真空泵抽速為常數,在管道直徑一定的情況下,當管道的長度變化時,其最大誤差亦發生較大的變化。
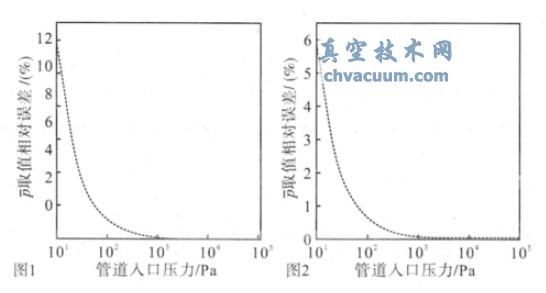
圖1 相對誤差隨著管道入口壓力的變化曲線(長管)
圖2 相對誤差隨著入口壓力的變化曲線(短管)
當D=0.04 m,S=8 L/s 時,近似把管道入口壓力取值為平均壓力時,其相對誤差隨著管道入口壓力、管道長度的變化如圖3 所示。從圖可以看出,隨著管道長度的變化,其最大誤差也逐漸增大,當L=5 m 時,最大相對誤差達到了45%。所以,若是管道太長,近似取值法是不適用的。這主要是因為管道長度越長,管道的流導就越小,管道進口和出口的壓差變大,若是再使用近似取值法,相對誤差也會隨著管道長度增大而增大。

圖3 相對誤差隨著入口壓力和管道長度的變化
當D=0.04 m,L=1 m 時,近似把管道入口壓力取值為平均壓力時,其相對誤差隨著入口壓力、泵的抽速(在每一抽速下,視為常數)的變化如圖4 所示。從圖可以看出,隨著真空泵的抽速的變化,其最大誤差也逐漸增大,當S = 100 L/s 時,誤差達到了70%。所以,若是泵的抽速太大,近似取值法是不適用的。
綜上所述,在計算粘滯流態下真空管道的流導時,當管道較短、泵的抽速較低、入口壓力較高時,管道平均壓力近似取值的相對誤差較小,反之,相對誤差較大。所以在計算粘滯流態管道的流導時,應該根據具體情況分析是否可以近似取抽氣管道入口處壓力為平均壓力。
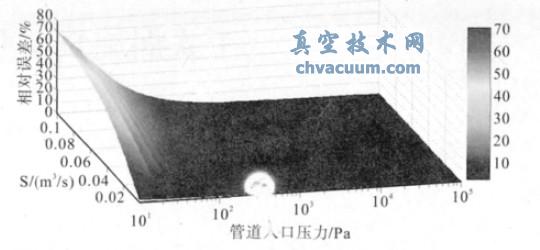
圖4 相對誤差隨著入口壓力和泵抽速的變化
在流導計算過程中,可以根據真空泵的抽速曲線數值化后的數組來假定在對應壓力范圍內真空泵的抽速為常數,然后采用式(2)、式(3)計算出管道出口處的壓力p2,根據式(1)計算出管道的平均壓力p,再計算粘滯流態下管道的流導,從而減少計算粘滯流態下管道流導的誤差。