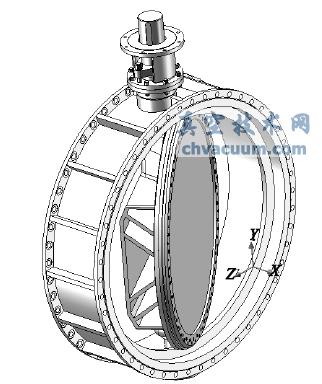
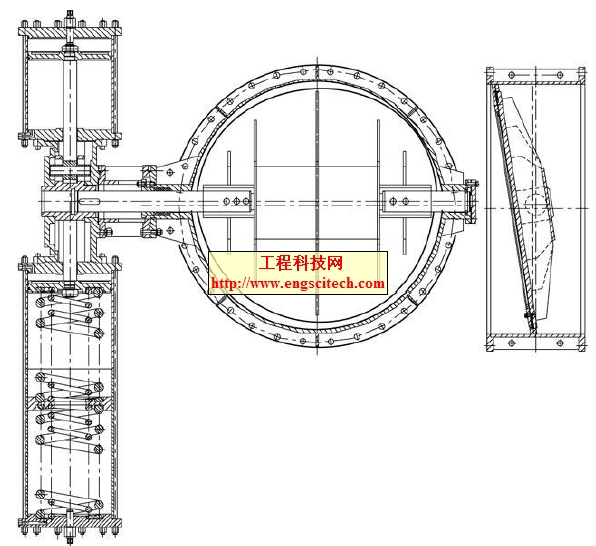
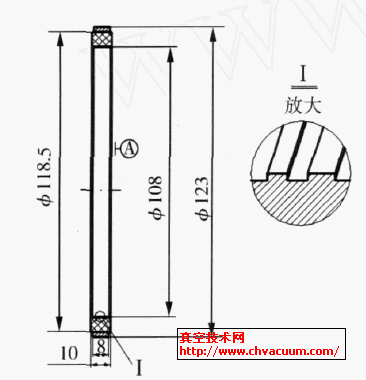
三偏心蝶閥密封面聯動磨削的運動特性分析
三偏心蝶閥密封面的形狀尺寸和表面質量是影響其密封性能的關鍵要素,密封面的高質量加工一直也是各廠家的難點。在傳統的空間幾何理論分析基礎上以閥體密封面的聯動磨削為研究對象,闡述了砂輪與工件的運動特性關系。
一、前言
三偏心蝶閥作為一種高性能閥門,在各個行業應用越來越廣,對其密封面的質量要求也越來越高,密封面的高質量加工一直是國內行業中的難點,各企業對三偏心蝶閥密封面的磨削方式基本上還處于摸索階段,尤其是聯動磨削在國內基本上沒有成功的案例。
二、密封面成形分析
由于三偏心蝶閥密封面形狀的特殊性,密封面為一個圓錐的斜截面,傳統的研磨方法在其上都不易實現,對密封面的最終成形國內的廠家基本上都是采取的車削方式。車削加工的局限性致使了產品性能無法進一步提高,研究新的磨削設備與磨削方式,提高產品的密封性能一直是各個廠家正在研究的課題。
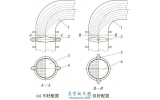
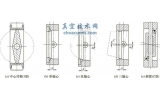
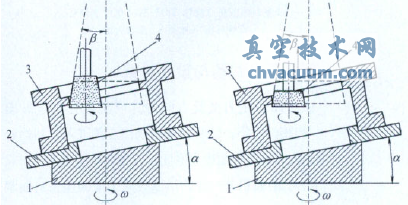
以下列舉了四種密封面成形的磨削方式,如圖1所示。從圖中可以看出四種磨削運動過程各有特點。圖1a為采取成形砂輪,砂輪面完全覆蓋磨削軌跡,磨削過程為砂輪旋轉運動的同時進行橫向進給。圖1b同樣為采取成形砂輪,砂輪面略大于閥體密封面寬度,磨削過程為砂輪旋轉運動,同時沿密封面圓錐母線進行上下運動(角度插補),并進行橫向進給。圖1c為采取傳統平行砂輪,砂輪主軸旋轉一定角度(密封面圓錐母線平行),砂輪面覆蓋磨削軌跡,磨削過程為砂輪旋轉運動,并進行橫向進給。圖1d為同樣采取傳統的平行砂輪,砂輪主軸旋轉一定角度(密封面圓錐母線平行),砂輪面略大于閥體密封面寬度,運動過程為砂輪旋轉運動,同時砂輪沿圓錐母線上下運動并與密封面同步(即運動過程中砂輪面不脫離閥體密封面),并進行橫向進給,即砂輪與工件進行聯動磨削。四種磨削方式各有其優缺點,同時對機床的要求也各不相同。圖1a到圖1c的運動過程相對比較簡單。圖1a與圖1c密封面的最后成形完全取決于砂輪面本身的形狀,同時在磨削過程中工件對砂輪的反作用力的著力點時刻在變化,砂輪主軸容易疲勞破壞。圖1b在磨削過程中為斷續磨削,存在沖擊,砂輪主軸容易疲勞的同時閥體密封面的成形也不是很好。圖1d為砂輪與工件進行聯動磨削,沒有圖1a到圖1c的影響,砂輪主軸受力恒定且不存在沖擊。但是要完成此聯動磨削,并不容易,一是對機床的要求比圖1a到圖1c的要高,機床c軸(工作臺主軸)能準確定位,且能與z軸能建立聯動關系,同時機床b軸(主軸的旋轉軸,即形成β角)定位準確。二是聯動運動相對復雜,完成聯動數控編程必須要有明確的幾何數學關系。所以求解砂輪移動速度v與工件的旋轉角度θ的幾何數學關系是完成聯動磨削的必要條件。所以以下著重對圖1d的聯動磨削運動特性進行分析研究。
(a)磨削方式1 (b)磨削方式2
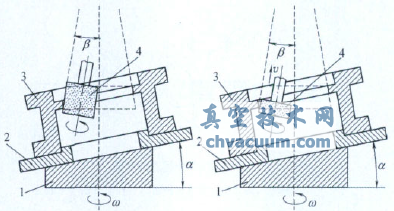
(c)磨削方式3 (d)磨削方式4
圖1 密封面成形的磨削方式
1.斜模2.工裝定位板3.閥體4.砂輪
三、砂輪與閥體密封面聯動運動特性分析
取圖1d中的密封面最低點為研究起始點,為了便于研究砂輪的運動方程,以圓錐中心線為z軸,密封面的最低點所在的平面為xy平面,且最低點在x軸上,建立坐標系,如圖2所示。H為圓錐的高度,R為圓錐的底半徑,即密封面最低點到工件旋轉軸z軸的距離。△ACC1為斜模平面,∠OAC=α(斜模角),∠AMO=β(圓錐半錐角),弧ABC為斜模平面與圓錐面的交線,即為砂輪運動軌跡(也為閥體密封面)。△MOB1為工件(或C軸)從初始點旋轉角度q時所在的位置。旋轉角度q所用時間為t,則動點b為此時的砂輪位置。假定動點B在z軸上的投影為B2,則B點到z軸的動半徑R(θ)=BB2,B點在z軸上的投影高度z(θ)=OB2。令B點在x與y軸方向的坐標分別為x(θ)與y(θ),則R(θ)=[x(θ)2+y(θ)2]。令M(θ)為砂輪在圓錐母線B1M方向位移,v為砂輪在圓錐母線B1M方向上的速度,ω為工件旋轉角速度,由幾何關系可知:
實際的加工過程中,R、ω、α和β均為已知常數,所以v=v(θ),對其用MATLAB進行計算分析得出其v—θ曲線如圖3所示,從v—θ曲線圖中可以看出,v與θ是非線性關系,而是速度v相對工件旋轉角度θ成正弦規律變化。明確了兩者之間的真實關系之后,便可為數控編程提供正確聯動數學模型,使聯動磨削得以實施。
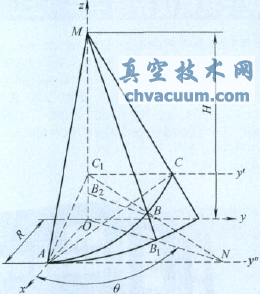
圖2 運動特性幾何分析
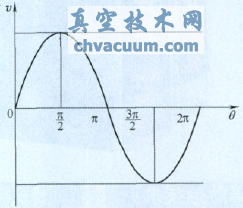
圖3 v-θ曲線
四、結語
通過對砂輪的運動特性研究分析,對數控編程進行數學幾何關系指導,使三偏心蝶閥密封面的聯動磨削成為現實,同時砂輪的不間斷磨削不僅將使磨削效率明顯提高,并且聯動磨削過程中砂輪受力恒定,對密封面的最后成形精度非常有利,新的磨削方式對研究純金屬硬密封三偏心蝶閥的零泄漏具有重要的意義。