參照墊片密封及閥座密封比壓原理，從力學角度建立閥門漏率計算公式，并以有限元方法建立閥門漏率計算模型，從而實現了閥門漏率的初步量化分析和計算。以充氣閥為例分析閥座結構尺寸對閥門密封性能的影響，結果表明在保證閥門非金屬面沒有破壞的前提下，閥座半徑越小越有利于閥門密封。

　　閥門是火箭增壓輸送系統重要元件，其工作環境惡劣( 較高的隨機振動量級，以及較寬的范圍) ，使用要求較高( 高壓、低壓均要求較高的密封性能) 。由于這些嚴酷的環境條件，閥門一直是運載火箭增壓輸送系統的一個薄弱環節，歷史上增壓輸送的多次故障與閥門漏率超標直接相關，而閥門密封性能的優劣則取決于閥座、閥芯密封配合副的設計。因此真空技術網(http://smsksx.com/)認為研究閥座結構尺寸對閥門密封性能的影響對提高閥門密封性能及增壓輸送系統可靠性具有重要的實踐意義。以往閥門閥座密封配合副設計( 不僅僅是結構設計) ，主要使用經驗公式計算主要技術參數，再通過試驗進行驗證和修改完善，這種方法研制周期長、效率較低。新研型號閥門介質壓力大為提高( 由23MPa 提高到35 MPa) ，且涉及常、低溫，這就更加增大了閥門密封的設計難度。

　　本文作者基于理論分析建立閥門漏率計算模型，并基于有限元分析軟件，分析閥門閥座結構尺寸對密封性能的影響，為型號閥門的研制提供技術參數。

1、活閥密封性能的研究方法

　　目前對于密封性能的研究還處于定性分析階段，設計手冊普遍將密封比壓作為密封優劣的判斷標準。但是對于R 形閥座、變形較大的非金屬密封面而言，其密封壓力具有高度的非線性，且沿活閥徑向密封壓力分布梯度較大，無法用現行的理論公式統一化處理。而對于密封漏率計算，墊片的漏率計算已經取得了一定的進展，本文作者擬參考墊片漏率的計算公式，建立閥座漏率計算的量化模型。對于墊片密封，其漏率計算公式為

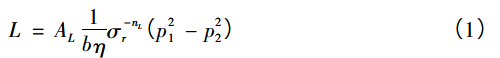
　　式中: AL、nL為常數; b 為墊片寬度; L 為墊片單位外周長的泄漏率; σr為接觸壓力; p1為介質壓力;p2為環境壓力; η 為系數。

　　將閥座密封實際情況與墊片的漏率計算公式進行對比，可以發現閥座的漏率計算更貼近墊片的漏率計算公式，與最大接觸壓力成反比，與密封面兩側壓力的平方差成正比。由此得到閥座密封漏率的近似關系為

　　式中: AL、nL為系數，需通過試驗測定; σr為接觸壓力; p1為介質壓力; p2為環境壓力。

　　從式(2) 計算得到的漏率與閥門漏率的變化趨勢是一致的，但公式的準確性還需大量的試驗數據進行驗證，由于試驗工作量大，周期長，相關工作還在進行中。基于墊片的漏率計算公式(2) 和傳統的密封比壓設計理論，則可以將對閥門密封性能的研究轉化為對閥座密封結構最大接觸壓力的研究，而密封結構的最大接觸壓力及密封比壓是可以通過有限元軟件對其進行量化分析的。本文作者通過有限元分析軟件，以最大接觸壓力為基礎并結合密封比壓建立閥門漏率計算模型，分析閥門結構形式及尺寸對閥門密封性能的影響，探索閥門密封的量化研究。

2、活閥密封結構的有限元力學模型

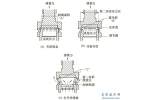
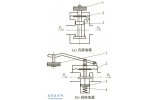
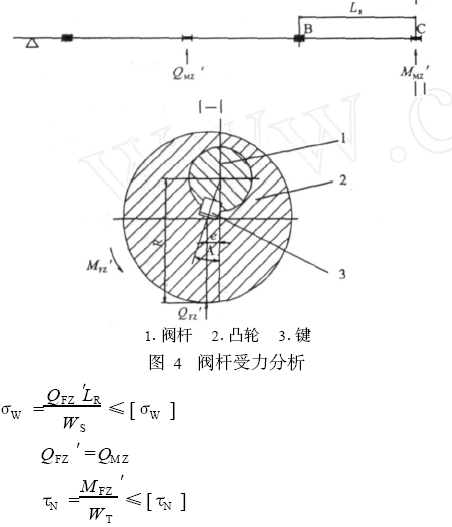
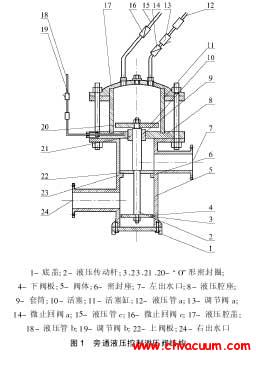
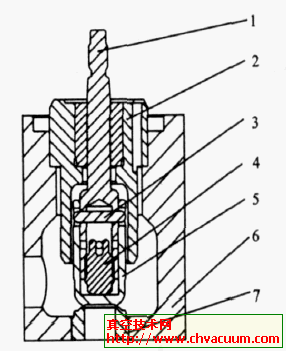
　　在目前常用的密封結構中，閥座基本為金屬材料，活閥密封面為非金屬材料，密封槽為金屬材料。金屬材料的剛度要遠大于非金屬材料，所以在建模時，可以將金屬材料結構看作剛體，減少計算量。另外活閥為回轉體結構，其載荷、邊界條件也是軸對稱的，因此可以將活閥簡化成軸對稱模型。活閥簡化后的力學模型如圖1 所示。

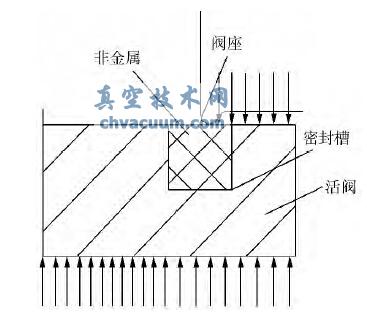
圖1 活閥軸對稱力學模型

3、結論

　　(1) 參照墊片密封及閥座密封比壓原理，從力學角度建立了閥門漏率計算公式，并以有限元方法建立閥門漏率計算模型，從而實現了閥門漏率的初步量化分析和計算。

　　(2) 從分析結果看，非金屬密封面與閥座的接觸寬度b 并不是常量，它隨著加載時間是不斷變化的，并且接觸壓力沿徑向梯度較大; 最大接觸壓力隨加載時間的變化與非金屬密封的實際工作情況接近;綜合以上因素，本文作者提供的閥門漏率的計算方法更接近實際，誤差更小。

　　(3) 在保證閥門非金屬面沒有破壞的前提下，閥座半徑越小越有利于閥門密封。