單座式調節閥閥芯-閥桿系統流固耦合振動研究
針對單座式調節閥閥芯-閥桿系統的流固耦合振動問題,建立了考慮閥門定位器作用的系統動態仿真模型,給出了求解閥芯-閥桿系統響應的預估-校正算法,利用ANSYS軟件對系統在固定開度與變開度情況和流開型與流閉型情況下的振動響應進行了定性分析。研究表明:對于固定開度,閥芯穩態位移偏移量以及流體力隨壓差增加以及開度減小而增大,閥芯動態位移過渡時間隨壓差增加而縮短,而流開型流向時閥芯位移響應幅度要大于流閉型流向。對于開度減小情況,采用流閉型流向時閥芯動態位移過渡時間更短,且壓差越大,閥芯動態位移過渡時間越短,而流開型流向時則相反;對于開度增大情況,閥芯動態位移過渡時間和壓差之間的關系與開度減小情況相反。
調節閥在水利、電站、化工、石油、冶金等過程控制系統中起著重要作用,然而調節閥在某些工況下產生的振動往往成為引起各種事故的主要原因,振動嚴重時甚至影響系統安全平穩地運行。導致調節閥振動的主要原因是閥體內部流體流動的不穩定性,與流固耦合作用直接相關。
流固耦合導致的調節閥振動可以分為兩種:一種是調節閥整體在管道上的振動;另一種是本文要研究的調節閥自身閥芯-閥桿系統振動。國內外有關閥流固耦合振動的研究較少,且大多偏重于在某些固定開度、單一流向工況下分析閥體及流道內的瞬態流場及其與閥體或閥芯、閥桿的彈性振動之間的流固耦合相互作用,例如分別對調節閥、電磁閥、截止閥、換向閥以及溢流閥等不同類型的閥的動態特性與流固耦合問題進行了仿真和試驗研究。
本文以某型號單座式調節閥為對象,研究調節閥閥芯-閥桿系統在流開式與流閉式流向、固定開度與變開度工況時的流固耦合振動問題。通過建立考慮定位器作用的系統有限元流固耦合模型并進行仿真,分析流開型和流閉型調節閥閥芯-閥桿系統在固定開度和變開度條件下的動態響應。
1、閥芯-閥桿系統動力學模型
1.1、單座式調節閥結構
單座式調節閥整體結構如圖1所示,主要由執行機構和調節機構組成。執行機構將控制器輸出電流信號轉換為調節閥閥桿的直線位移;調節機構通過閥桿與執行機構相連,并將位移信號轉換為閥芯和閥座之間流通面積的變化,從而改變流經閥體的流體運動狀態。為了使閥芯和閥座之間的開度穩定在某個特定位置以保證實現控制器所要求的目標狀態,調節閥設有閥門定位器附件,組成以閥桿實際位移為測量信號、以控制器電流輸出為設定信號的反饋控制系統。
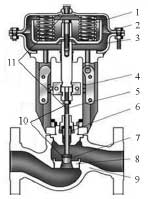
圖1 單座式調節閥結構示意圖
1.彈簧2.膜片3.氣室4.位移刻度5.閥桿6.填料7.閥芯8.閥座9.閥體10.調節機構11.執行機構1.2 閥芯-閥桿系統動力學模型
閥芯-閥桿系統是調節閥執行-調節機構的主體,主要包括薄膜膜片、推桿、彈簧、填料、閥桿、閥芯和閥座等,如圖1所示。
對于特定調節閥結構,其調節性能主要取決于閥芯-閥桿相對閥座的運動。閥芯-閥桿與氣室彈簧、填料、流體等組成一個流固耦合動力學系統。在建立閥芯-閥桿動力學模型之前作如下假設:調節閥內部的流體(水)是不可壓縮的;在調節閥工作過程中,水沒有熱交換;閥桿與填料之間的摩擦力認為是一種粘性阻尼力;整個閥體為剛性體,忽略其彈性變形;閥芯-閥桿只沿軸線運動,不考慮橫向運動;單座閥的執行機構為氣動正作用執行機構。
根據以上假設以及單座閥的結構圖,可以將閥芯-閥桿系統簡化為一個單自由度質量-彈簧-阻尼系統,如圖2所示。閥芯位移坐標原點設在閥門全關的位置,取向上為正方向。
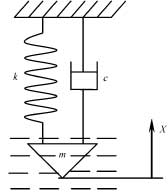
圖2 閥芯-閥桿系統動力學模型
根據圖2所示,單座閥閥芯-閥桿系統動力學方程為
———閥芯t時刻的位移、速度及加速度
m———閥芯-閥桿系統的總質量
k———彈簧剛度系數
c———等效粘性阻尼系數
Fc(t)———執行機構作用在閥芯上的控制力
Fl(t)———流體不平衡力
g———重力加速度
式(1)中流體不平衡力Fl(t)(以下簡稱流體力)是指行程調節機構中流體作用在閥芯上的軸向合力,其大小與調節閥兩端的壓差、閥芯大小和形狀、調節閥類型、閥上游壓力、流體流向及流體物理特性等因素有關。對于流開式流向(圖1中流體從左側流入,右側流出),流體力為
式中 p1———閥前壓力 p2———閥后壓力
Δp———前后壓差 ds———閥芯直徑
dz———閥桿直徑
對于流閉式流向(圖1中流體從右側流入,左側流出),流體力為
對于動態問題,無論流開式還是流閉式流向,閥芯受到的實際流體力Fl(t)由閥芯上下分布的壓力(通過預估-校正有限元流固耦合計算)對閥芯表面面積積分求得。為了使求解過程簡化,可以將流體力近似認為流體壓力在閥芯等效橫截面積上作用的結果。
式(1)中控制力Fc(t)是指執行機構作用在調節機構閥芯-閥桿系統上的軸向力,其大小與電-氣閥門定位器結構參數、控制器輸出電流信號產生的電磁力以及閥芯位移有關。閥門定位器是調節閥的主要附件。它將閥桿位移信號作為輸入的反饋測量信號,以控制器輸出信號作為設定信號,將二者進行比較,當兩者有偏差時,改變其到執行機構的輸出信號,使執行機構動作,從而建立了閥桿位移信號與控制器輸出信號之間的一一對應關系,即
式中 p、q、T———與定位器結構性能有關的參數
N(X0)———與指定目標位移X0成比例的電磁力
因此,調節閥閥芯-閥桿系統動力學方程可寫為
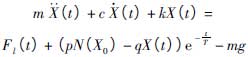 (5)
(5)2、閥芯-閥桿系統流固耦合問題求解
由于前面建立的調節閥閥芯-閥桿系統動力學方程中的流體力Fl(t)無法用準確的解析表達式表示出來,需要通過有限元流固耦合方法計算得到。本文采用ANSYS12.0中的CFD模塊對調節閥內部流場進行分析計算,首先建立內部流場的幾何模型,然后對不同工況下的調節閥流場進行計算,求得流體力。調節閥內部流場幾何模型可以通過三維建模軟件SolidWorks來建立,計算流場時需要對ANSYS中的CFD模塊的流固耦合方法進行改進。
2.1、流固耦合分析典型步驟
通過ANSYS軟件物理環境方法對閥芯-閥桿系統進行流固耦合分析。閥芯-閥桿會在流體力作用下發生位移,位移的大小將改變閥芯移動壁面邊界,從而顯著影響流場的形狀。流固耦合分析通過在結構分析中得到閥芯移動壁面位移,用于流場分析。具體流固耦合分析的典型步驟如下:
(1)創建整個幾何模型:包括流體區域和調節閥閥體結構區域。
(2)創建流體物理環境:給流體區域賦予單元類型,還要確定迭代次數,激活湍流模型,施加邊界條件。
(3)創建結構物理環境:清除在流體物理環境中設定的信息,準備定義結構物理環境。轉換單元類型并設定單元選項,將流體區域單元設定為NULL,將結構區域賦予單元類型,施加結構邊界條件,定義合適的載荷步和求解選項,然后寫入結構物理環境文件。
(4)流體/結構求解循環:在本系統中,入口的速度作為總體收斂的準則。當兩次Flotran求解的入口速度差值足夠小時,求解結束。初始Flotran分析設置的迭代次數應當多一些,以利于較好地收斂。隨后的流體分析由于是在前一次流體分析基礎上重啟動,因此,迭代次數可以少一些。結構分析同樣也需要重啟動。對于非線性分析,節點必須在重啟動以前恢復到初始位置。本文計算一共執行了5次耦合迭代,第1次Flotran分析共迭代100次,以得到較高的收斂精度,隨后的4次Flotran分析各迭代40次,即可滿足精度要求。一共迭代260次,取前250次數據即前0.25s的位移響應。
2.2、閥芯-閥桿系統流固耦合模型預估-校正求解算法
由于調節閥閥芯與流場接觸面為移動壁面,ANSYS軟件的典型流固耦合方法難以滿足計算要求,本文采用預估-校正算法[8]來解決這種情況下的流固耦合問題。根據閥芯-閥桿系統動力學方程(5)和預估-校正算法,可得出閥芯-閥桿系統的預測步和校正步計算表達式,分別為
預測步
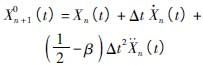 (6)
(6)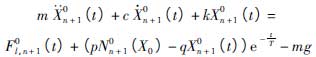 (8)
(8)第r步校正步
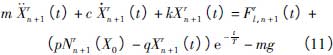
2.3、閥芯-閥桿系統流固耦合有限元模型建立
2.3.1、調節閥內部流場幾何模型創建
調節閥的內部流場就是調節閥內部充滿流體后所占的空間。假設閥體、閥芯是剛體,流場的邊界是閥體、閥芯與流體的耦合面,閥體與流體之間的耦合面是不動的,而閥芯與流體之間的耦合面是移動的(包括固定開度下的振動和變開度時的移動)。由于假設閥芯是剛體,所以在做流場分析時,需要將閥芯部分挖去,對于不同的開度,只需要將對應閥芯位移的不同位置挖去即可,由于閥桿對流場的影響比較小,所以在建立的模型中忽略閥桿。調節閥的內部流場模型如圖3所示。

圖3 調節閥內部流場模型
2.3.2、網格劃分
本文采用自由網格劃分方法。在劃分網格之前首先要設置單元類型,并為實體模型分配單元屬性,本文中的流場模型采用的是Fluid142單元。閥芯與流體之間的耦合面流場變化比較大,采用最大為0.002的網格劃分,而其他部位閥體與流體之間的耦合面,采用最大為0.004的網格劃分,根據劃分結果,共有單元102306個,節點20531個。網格劃分結果如圖4所示。

圖4 流場模型網格劃分
2.3.3、載荷施加
在網格劃分之后,要對模型施加載荷以及邊界條件,本文中對模型施加的具體條件如下:
(1)入口:定義壓力為0.2~2.1MPa。
(2)出口:定義壓力為0.1MPa。
(3)固定壁面條件:所有與閥體接觸的耦合面上流體流動速度為零,相對位移為零,即除了進出口端面和閥芯周圍的耦合面外,其余邊界上速度和位移均為零。
(4)移動壁面條件:與閥芯接觸的耦合面上的流體速度和位移應該與閥芯的運動速度和位移一致,即當閥芯靜止時,耦合面上的流體速度和位移均為零;當閥芯運動時,耦合面上每個節點的任何時刻的速度和位移大小都與閥芯上對應節點的速度和位移大小相同。由于本文只考慮閥芯軸向運動,所以以上提到的位移和速度均指軸向位移和軸向速度,其余方向的位移和速度都為零。
(5)不考慮溫度變化,即不涉及熱交換。
3、閥芯-閥桿系統流固耦合動態響應分析
通過求解閥芯-閥桿系統流固耦合模型,仿真計算調節閥在不同邊界條件下閥芯受到的動態流體力以及閥芯-閥桿系統的動態位移響應,分析定位器對調節閥閥芯振動的影響,考察閥內介質流向不同時,閥芯在固定開度和變開度的振動情況,找出閥芯受到的動態力與位移、壓差之間的關系。
3.1、閥門定位器對閥芯-閥桿系統動態響應的影響
假設閥芯在目標位移15mm處,分別在進出口壓差為0.1、0.5、1.0、2.0MPa下工作,介質流向為流開狀態,初始相對位移為-0.1mm,初始速度和加速度均為零,初始流體力為50N。分別對比分析帶有閥門定位器和沒有閥門定位器時閥芯-閥桿系統的閥芯位移和流體力響應,如圖5、6所示。
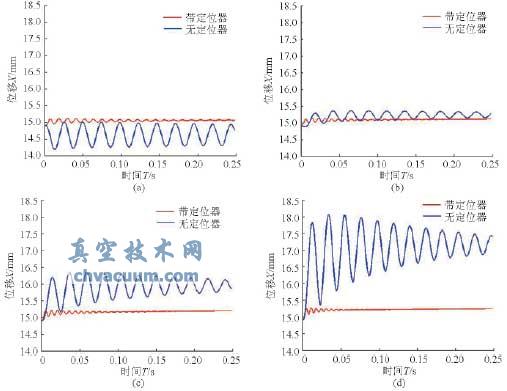
圖5 單座閥閥芯的振動響應對比
(a)壓差0.1MPa(b)壓差0.5MPa(c)壓差1.0MPa(d)壓差2.0MPa
由圖5可得:帶有定位器比無定位器時閥芯振動波動小得多,而且趨近目標平衡位置的時間更短。在較大壓差(0.5~2.0MPa)下,無論是否帶有定位器,壓差越大,閥芯振動偏離目標位置越遠,并且振幅越大,而帶有定位器的調節閥工作狀態更為穩定、精確。
由圖6可以看出:隨著壓差增大,無定位器的閥芯受到的流體力波動也隨之增大,而帶有定位器的閥芯受到的流體力變化則一直保持平穩,并且逐漸從小于前者的均值過渡到大于其均值。
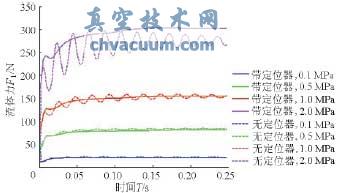
圖6 單座閥閥芯受到的流體力對比
3.2、單座閥在固定開度下的動態特性分析
假設調節閥閥門全關位置為坐標原點,取向上為正方向,總行程為0(全關位置)~25mm(全開位置),進出口壓差變化范圍為0.1~2.0MPa,介質流向分別為流開和流閉。考察閥芯在目標位移(指定開度)作自由振動時閥芯的振動情況。
3.2.1、不同流向對單座閥動態特性的影響
在某個目標位移下,閥芯在受到初始運動條件的擾動時,會在平衡位置作自由振動。假設閥芯分別在不同目標位移(3、5、10、15、20、25mm)下和不同進出口壓差(0.1、0.5、1.0、2.0MPa)下工作,初始相對位移為-0.1mm,初始速度和加速度均為0,不同工況下初始流體力不同,考慮定位器作用,得出介質流向不同時單座閥閥芯的位移與閥芯受到的流體力隨時間變化歷程。圖7為某固定開度(目標位移為10mm)時閥芯位移與閥芯所受流體力的時間響應歷程。圖8為位移、壓差與流體力的三維關系圖和二維關系圖(為便于比較,圖中流閉時的流體力均取正值表示)。
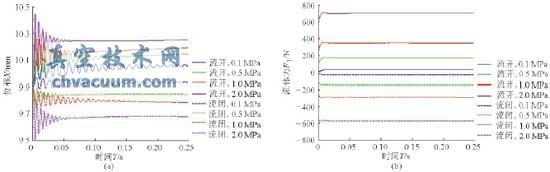
圖7 固定開度不同壓差下的振動響應
(a)位移響應(b)流體力響應
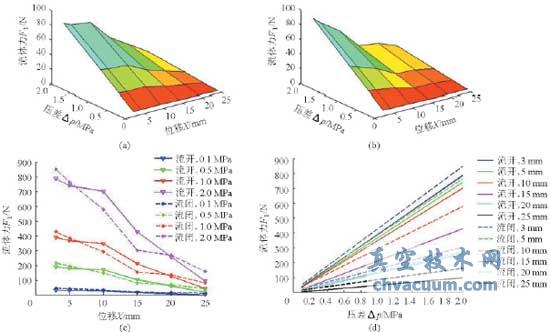
圖8 動態流體力與位移、壓差之間的關系
(a)流開狀態三維表示(b)流閉狀態三維表示(c)位移為參數(d)壓差為參數
由圖8可以看出:
(1)在不同的目標位移下,無論介質流向為流開或者流閉,流體力總是隨壓差增大而線性增長。
(2)在不同的進出口壓差下,無論介質流向為流開或者流閉,流體力隨著位移的增大(開度增大)而減小。
(3)在較小壓差(0.1MPa)下,流開狀態下的流體力總是小于流閉狀態下的流體力;在較大壓差(0.5~2.0MPa)下,在閥門接近全開和全關位置時,流開狀態下的流體力小于流閉狀態下的流體力,而閥門在中間位置時,流開狀態下的流體力大于流閉狀態下的流體力。
3.2.2、不同流向對閥芯位移偏移量的影響
閥芯在不同壓差下趨向目標開度的過程中,實際工作開度相對設置目標開度對應的閥芯位移之間有一定的偏移量。根據不同壓差、位移下閥芯運動仿真,可以得到不同介質流向時閥芯偏移量與壓差、位移之間的關系,如圖9所示(為便于比較,圖中流閉時的偏移量均取正值表示)。
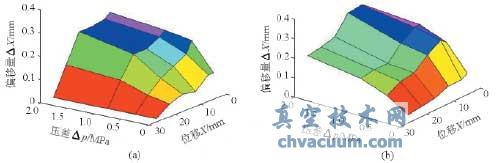
圖9 偏移量與壓差、位移之間的關系
(a)流開狀態(b)流閉狀態
由圖9可以看出:
(1)在較小壓差(0.1MPa)下,流開狀態下閥芯偏移量要比流閉狀態下的偏移量大;在較大壓差(0.5~2.0MPa)下,流閉狀態下的偏移量總體要比流開狀態下的偏移量大;且各種工況下的偏移量都在允許的范圍(3%~5%)內,能夠滿足定位精度。
(2)在同一個目標位置處,壓差越大,偏移量越大。
(3)在同一壓差下,目標位移越大,偏移量越小。
3.3、單座閥在變開度下的動態特性分析
閥芯在受到流體力和控制力作用時,會從初始位置向目標位置運動,并最終保持在目標位置附近作振動。假設閥芯運動過程為20~15mm(開度變小)和5~10mm(開度變大),進出口壓差分別為0.1、0.5、1.0、2.0MPa,初始相對位移為-0.1mm,初始速度和加速度均為0,不同工況下初始流體力不同,并考慮定位器作用,得出介質流向不同時單座閥閥芯的位移與閥芯受到的流體力隨時間變化歷程,如圖10、11所示。
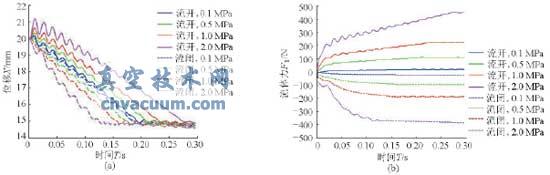
圖10 開度為20~15mm時在不同壓差下的閥芯振動位移和流體力
(a)位移響應(b)流體力響應
由圖10、11可以看出:
(1)閥芯位移從初始位置以振蕩衰減的方式到達目標位置,并在目標位置附近作自由振動。
(2)閥芯在向下運動減小開度過程(20~15mm)中,采用流閉流向比采用流開流向,閥芯到達目標位置所用時間更短;當介質為流閉流向時,壓差越大,閥芯達到目標位置所用時間越短,而介質為流開流向時,壓差越大,閥芯達到目標位置所用時間越長。
(3)閥芯在向上運動增大開度過程(5~10mm)中,采用流開流向比采用流閉流向,閥芯到達目標位置所用時間更短;當介質為流開流向時,壓差越大,閥芯到達目標位置所用時間越短,而介質為流閉流向時,壓差越大,閥芯達到目標位置所用時間越長。
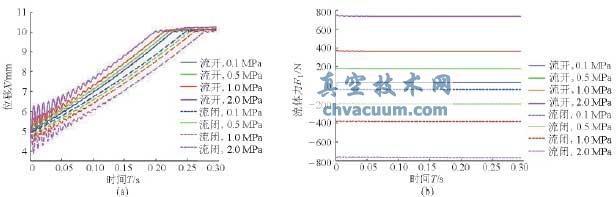
圖11 開度為5~10mm時在不同壓差下的閥芯振動位移和流體力
(a)位移響應(b)流體力響應
(4)閥芯在向下運動(開度減小)過程中,閥芯受到的流體力從初始位置以振蕩衰減的方式到達平衡位置,并在平衡位置附近振動,且到達平衡位置所用時間與位移到達目標位置所用時間相同;介質為流開流向時,壓差越大,閥芯受到的流體力達到平衡位置所用時間越長;介質為流閉流向時,壓差越大,閥芯受到的流體力達到平衡位置所用時間越短;總體上看,在同一壓差下,閥芯在流開流向時受到的流體力要比流閉流向時受到的流體力大。
(5)調節閥在向上運動(開度增大)過程中,閥芯受到的流體力始終處于平衡位置附近,并且在同一壓差下,閥芯在流閉流向時受到的流體力比流開流向時受到的流體力大。
4、結論
(1)建立了一個考慮定位器作用的調節閥閥芯-閥桿系統流固耦合動力學模型,并利用ANSYS軟件對固定開度和變開度情況、流體流向為流開和流閉情況進行了動態響應仿真分析。
(2)研究結果表明,閥門定位器具有減小閥芯位移振動響應和閥芯位移偏移量的作用,選擇合適的定位器參數可以保證調節閥動態性能處于良好狀態。對于固定開度情況,無論流閉型還是流開型流向,閥芯穩態位移偏移量以及流體力隨壓差增加和目標位移減小(開度減小)而增大,閥芯動態位移過渡時間隨壓差增加而縮短,而流開型流向時閥芯位移響應幅度要大于流閉型流向。對于開度減小情況,采用流閉流向相對流開流向時閥芯動態位移過渡時間更短,采用流閉流向時,壓差越大,閥芯動態位移過渡時間越短,而流開流向時則相反;對于開度增大情況,閥芯動態位移過渡時間和壓差之間的關系與開度減小情況相反。