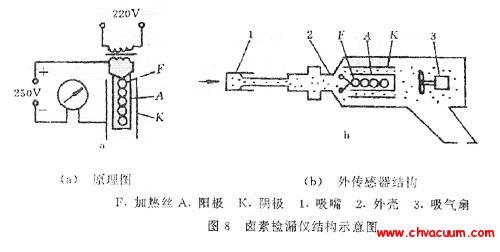
大型真空系統氦檢漏率的快速準確檢測方法
大型真空系統檢漏往往耗時長、效率低。本文分析了氦氣通過漏孔進入氦質譜檢漏儀形成檢漏信號的規律,并據此建立檢漏信號數學模型,確定漏孔的最終穩態泄漏信號。基于上述分析,提出漏孔漏率的一種快速預測方法。該方法用于大型真空系統檢漏能準確預測被檢部位的漏率,能顯著縮短檢漏時間,提高檢漏效率。
當前,大型真空系統被廣泛應用于航空航天、核電及高能物理等領域,為了確保這些系統能順利達到規定的真空度(及潔凈度),在合理設計真空獲得系統的基礎上,必須使裝置的泄漏低于允許限值。
大型復雜系統的氦質譜檢漏歷來是勞動強度大、專業素質要求高、耗時長而繁瑣的任務,某些應用領域對檢漏結果的準確性要求也很高。由于大型真空系統的響應時間長,所需持續施氦并監測的時間往往很長。為了實現漏孔的快速準確檢測,需采用一種既不影響檢漏靈敏度,又能縮短檢漏時間、提高檢漏效率的方法。本文分析了檢漏信號的形成過程、檢漏數據變化規律,建立動態氦質譜檢漏信號的數學模型,基于該模型進行數據擬合分析推算,提出一種漏率快速準確檢測的方法。
1、氦質譜檢漏信號分析
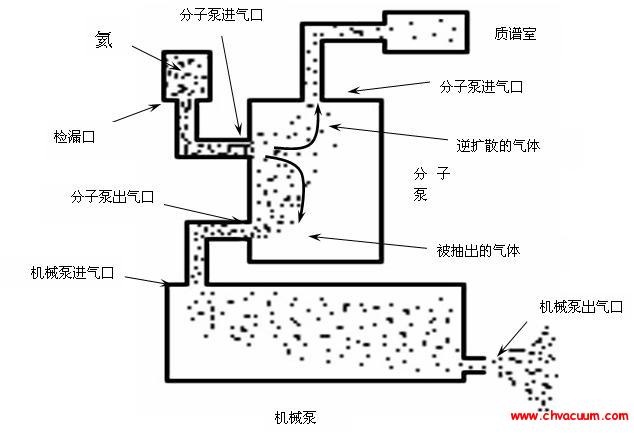
以單一漏孔(可看作一條粗細均勻的圓管)的氦泄漏信號為例,分析檢漏信號的形成規律。檢漏儀質譜室中氦分壓建立是一個動態過程:氦氣通過單一漏孔直接進入到檢漏儀,一部分在檢漏儀質譜室中建立氦分壓,另一部分被真空系統抽走。氦分壓與單位時間進入質譜室的氦氣量、檢漏儀質譜室處的氦抽速有關。當初始氦分壓為零或可以補償至零時,其函數關系見式(1)。

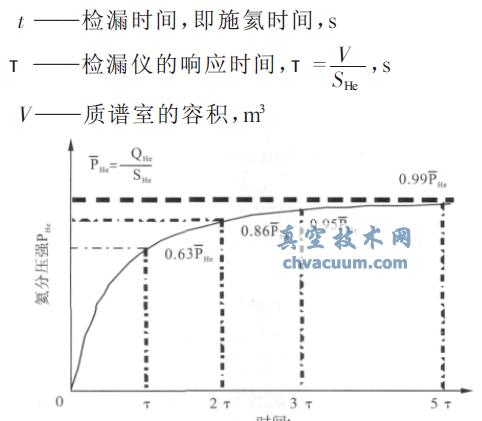
圖1 檢漏信號變化特征曲線
公式(1)反映了檢漏儀質譜室內氦分壓與時間的關系,而檢漏儀測量信號同質譜室內的氦分壓線性對應,也具有同樣的變化規律。當本底為零時,檢漏信號與噴氦或充氦后的檢漏時間有如下關系:
(1)施氦最初t=0,檢漏信號為0;
(2)檢漏信號隨噴氦檢漏時間延續而增大,檢漏時間足夠長,即t→∞ 時測量信號達最終穩定值,也是最大值QHe/SHe;
(3)系統反應時間τ 決定檢漏信號變化的快慢。檢漏時間持續到系統反應時間τ 的3 倍時,測量信號將達到最終穩定值的1- e- 3=95%;檢漏時間持續到系統響應時間的5 倍時,測量信號將達最終穩定值的1- e- 5=99%,此后繼續延長檢漏時間,測量信號的增量也不會超過最終穩定值的1%。
通常對檢漏結果不確定度沒有特殊要求的情況下,為了提高檢漏效率,持續施氦時間超過檢漏真空系統響應時間3τ 后,即確定測量信號已達到最終穩定值的95%以上,則可以讀取檢漏信號。實際檢漏過程中,受檢漏系統最小可檢漏率δQ 所限,當充氦時間足夠長以致儀器無法分辨氦泄漏信號的微小增量時,檢漏儀就會以一個穩定的示值輸出。通常情況下該穩定示值與漏孔真實漏率的偏差小于δQ/Q0×100%。也就是說,檢漏結果同漏孔真實漏率的偏差不僅與施加示漏氣體后讀取信號的時機有關,也與系統的最小可檢漏率相關。根據密封安全要求,合理確定檢漏方法、搭建檢漏系統并標定后,檢漏結果的精準度主要取決于持續供氦后的監測時間[5~6]。
2、漏率快速準確檢測方法探討
基于上述檢漏儀實測信號的分析,對于大空腔抽真空檢漏,檢漏真空系統的響應時間較長,由公式(1)和圖1 可知,檢漏信號若要達到絕對穩定所需持續供氦與監測的時間很長。為了保證檢漏結果的準確性,即便監測時間設定為3 倍的系統響應時間,完成檢漏仍將需要很長的時間。實際上對于單一漏孔,其檢漏信號有典型規律可循(上節已作詳細分析),如果能根據前期較短時間的檢漏數據及其信號規律來預測出測量信號的最終穩定值,對被檢漏孔的漏率做出準確預估,理論上是完全可行的,從而不必保持很長的供氦及候檢時間來等待儀器示值最終穩定。這種漏率快速檢測方法將顯著提高大空腔抽真空檢漏的效率。
3、應用實例
在某大容器整體負壓檢漏中,因系統響應時間較大,該容器上某被檢部位的檢漏信號呈緩慢上升趨勢。按上述漏率預測方法,分別取前15 min和35 min 的檢漏數據,采用一階指數衰減函數模型對該檢漏信號擬合,繪制曲線見圖4。其中,L5 為實測數據連線,L6、L7 分別是用前15 min 和35 min 的檢漏數據進行一階指數衰減擬合獲得的曲線。
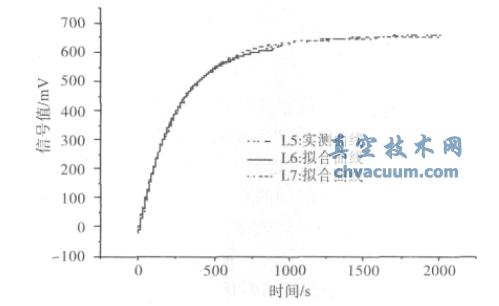
圖4 某大容器實測檢漏信號及其擬合曲線
由擬合結果分析可知,按前15 min 和35 min的檢漏數據進行擬合,求得檢漏信號(即A1 值分別是652 mV 和658 mV) 同實際測得檢漏信號(662mV)之間的相對偏差均小于2%。根據擬合與實測所得的檢漏信號同標準漏孔校準信號比對,求得被檢部位的最終穩定漏率均為1.4×10- 8 Pa·m3/s。
這就是說,對于這種簡單漏孔,在準確掌握其檢漏信號形成規律的前提下,根據前15 min 的檢漏數據可以準確預知其實際漏率;持續延長泄漏監測的時間,檢漏最終結果的準確性改善程度有限。
4、結束語
根據上述理論分析、實驗研究及實際應用情況,本文提出以下漏率快速準確檢測方法:在能夠準確掌握漏孔的氦泄漏信號形成規律前提下,通過建立其數學模型,代入早期足量檢漏數據以擬合分析出檢漏信號的時間函數,實現漏孔漏率的準確速判。這將顯著提高大型真空系統的負壓檢漏效率。