本文通過真空背景溫度，定義了真空背景周期。并從理論上指出，真空介電常數等于真空背景周期的二分之一。同時，真空電阻率應為1。

一、定義真空背景周期

　　我們知道，真空環境下的溫度為T=2.725開。其乘上玻爾茲曼常數K即可表示真空中微粒的平均能量。由于KT表勢能，hυ也表勢能。其中，h為普朗克常數，υ表頻率。

　　又由于頻率υ為周期t的倒數，故有

　　hυ=KT⇒h/t=KT⇒t=h/KT

　　把h=6.626×10^-34，K=1.3807×10^-23，T=2.725代進去，得：t=h/KT=1.762×10^-11(秒)。

　　真空技術網(smsksx.com)暫把這個周期稱為真空背景周期。它表示在真空背景溫度下微粒的平均運動周期。

二、真空介電常數的本質

　　物理上，真空介電常數是一個重要常數，用 ε₀表示。

　　我們假設一正一負兩電荷(電量為e)在相距距離為r的地方“靜止”。其勢能為：

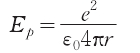
　　應指出，兩電荷“靜止”不代表其絕對靜止，它們也在真空背景溫度下悄悄運動。這個運動可看成簡諧運動(也可用圓周運動來描述)，周期為t。因此，某個電荷要產生電流I，且I=e/t。

　　由于電荷運動其電場也跟著變化(指空間靜止某點的電場強度變化)，又位移電流的本質是變化電場，所以這種變化的電場就會在兩電荷之間傳遞，形成電流。此處的位移電流周期也為t，大小也為I=e/t。因為位移電流的表述式可寫為：

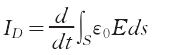
　　這里，E為電場強度，S為截面積，∫S為面積分。

　　式子右邊的積分可等電量Q，因此此式仍滿足I=dQ/dt的關系。而這里I=e/t是從I=dQ/dt定義式推出，因此，I=e/t，可表示這里的位移電流在空間分布的大小。

　　我們再根據相對性原理得出，任何物理規律都有相同的數學表達式，因此，某電流所受的電壓(或電勢)e/ε₀4πr 也應滿足歐姆定律U=IR，U為電壓，R為電阻。

　　又：R=ρl/s

　　其中，ρ為電阻率，l為電流長度，s為截面積。對兩點電荷來說，l=r，s=2πr²，因為位移電流的長度即為兩電荷間距離。應注意的是，截面似乎應是球面積4πr²，但其實不是。我們可作這樣分析：假設左邊電荷帶正電，右邊電荷帶負電，又假設右邊負電荷不存在時，左邊正電荷的電場線是以球面積發散，我們把這個球面分為左、右兩個半球面。當右邊有了負電荷時，正電荷的電場線應該幾乎全部向右邊半球指向(因為正電荷指向左邊的電場線，這時也會受負電荷影響，也會迂回向右指向)，又由于位移電流是變化電場，那么變化電場這種電流就幾乎全集中在右邊半球，而左邊半球幾乎無電流，那么左邊半球面對電阻就應無貢獻。因此，正電荷的電阻就應取右邊半球，其截面為半個球面，即2πr²(當然，也可用其它方法分析，結論一樣)。

　　我們又知道，根據量子力學觀點，導體的電阻是由其內部的雜質而引起，而對于真空來說，其中沒雜質，因此，真空的電阻只有幾何因素，沒有物質結構因素(電阻率)，或者說真空沒有電阻率這個概念，真空的電阻率可看作1，沒有轉化系數。對于兩點電荷來說，其位移電流的電阻為：

　　這和實驗值 ε₀=8.85×10^-12相比較，基本相符。說明了推導的可行性。

　　真空介電常數本質上應是時間的量綱。

小結

　　前面所述，可能真空電阻率取1這一點，較難理解，我們這里也可這樣說明：真空電阻率肯定是一個確定的數。我們若把真空電阻率取除1以外的任意數時，我們都不能用理論或邏輯推導計算出它，因為電阻率與物質結構有關，而真空沒有物質結構，它的存在沒有道理。所以，真空的電阻率只能取1。

　　另外，本文計算真空介電常數時，理論值和實驗值有大約有1/200的誤差，這時由于：如正電荷的電場線在負電荷存在時還是有少量的向左邊半球指向，考慮上這個因素，前面的計算值只能比實驗值稍小。但文中所述道理卻是成立的。所以，誤差也可修正。讀者可判斷這方面。關于說明真空介電常數的本質，作者是有把握的，這些有很多應用，如分析霍耳電阻。讀者可進行思考。具體內容本文就不敘述了。