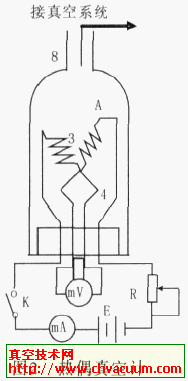
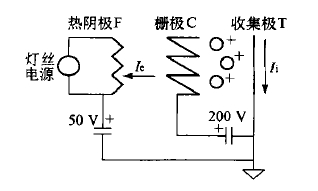
真空計現場校準不確定度分析
給出真空計現場校準的完整不確定度描述,列出了校準過程中詳細的影響因素,幫助解決真空計現場校準過程中不確定度的計算問題,并通過實際案例分析,將最終測量結果控制在合理而有效的范圍之內。
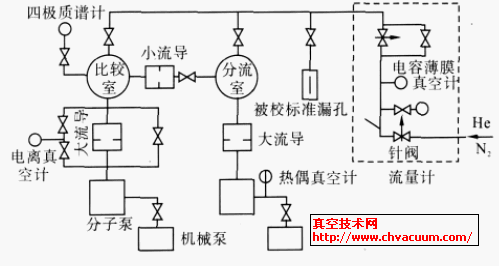
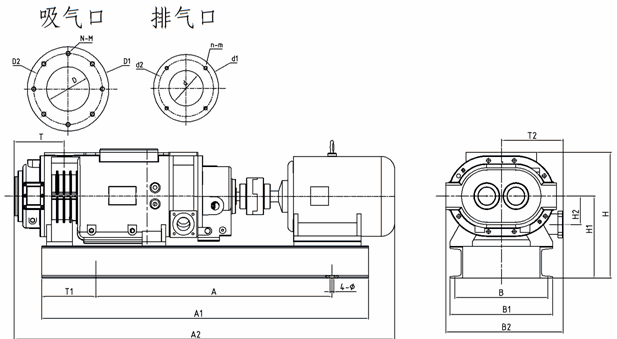
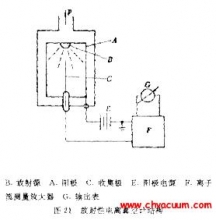
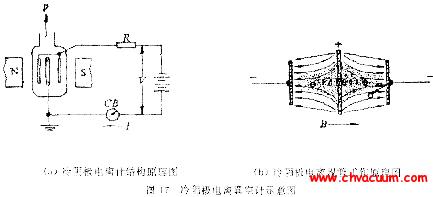
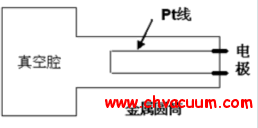
真空計是用來測量絕壓狀態下大氣壓力的儀器,廣泛運用于軍工、電子、醫療食品、電力、冶金、化工等各種領域。隨著科技的發展,行業中對真空計的要求也在不斷地提升,精度已普遍達到10-2Pa 左右。由于真空系統是包含真空規管、真空泵(羅茨泵、機械泵、分子泵等) 、各種連接管道以及真空擋板閥門在內的一套完整的測試系統,體積龐大,且在現場安裝位置固定,無法實現對真空系統的實驗室校準,現代化的集成生產逐漸要求對真空系統進行現場校準。對真空系統的現場校準也是今后真空校準的發展趨勢。
真空計現場校準過程中很重要的方面就是校準不確定度問題。由于現場條件多變,環境參數不穩定,因此相對于實驗室校準,現場校準的不確定因素更多,情況更加復雜,需要考慮更多的不確定度影響因素,以取得合理的校準結果。
1、真空計現場校準模型分析
下面對于10-3 ~105Pa 的真空計現場校準的不確定度作出分析。
對于現場校準的真空計,其修正值的計算公式如下:
K = pstd - psys - puuc (1)
式中:K 為真空計示值修正值,Pa;pstd為標準壓力值,Pa; psys為系統補償值,Pa;puuc為被測真空計示值,Pa。
根據公式(1) 可知,影響真空計現場校準的不確定度因素主要包括標準器、被測真空計以及校準系統三個方面,其中每個影響量又包含若干個影響因素。下面分別就標準器、被測真空計以及校準系統引入的不確定度作單獨分析。
1.1、標準器引入的不確定度
標準壓力值pstd由以下公式給出:
pstd= pref - pz + δp1 + δp2 + δp3 + δp4 + δp5 (2)
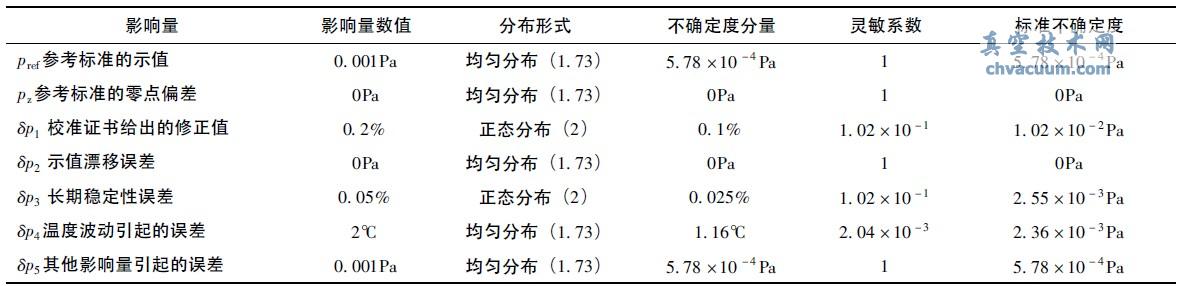
式中:pref為參考標準的示值,Pa;pz為參考標準的零點偏差,Pa;δp1為校準證書給出的修正值,Pa;δp2為示值漂移誤差( 多數情況下此值為0) ,Pa;δp3為長期穩定性誤差,Pa;δp4為溫度波動引起的誤差,Pa;δp5為其他影響量引起的誤差,Pa。所以,由標準器引入的標準不確定度為:
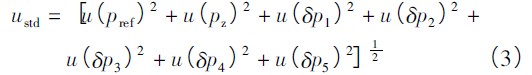
1.2、被測真空計引入的不確定度
被測真空計值由下式給出:
puuc = pind - p0 + δp6 + δp7 (4)
式中: puuc為被測真空計值,Pa;pind為被測真空計顯示值,Pa;p0為被測真空計零點偏差,Pa;δp6為被測真空計漂移誤差,Pa;δp7為被測真空計其他影響量誤差,Pa。
所以,被測真空計引入的標準不確定度為:
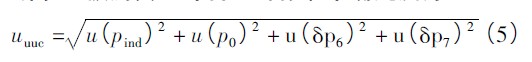
1.3、校準系統引入的標準不確定度
校準系統引起的影響量為:
psys = δp8 + δp9 + δp10 (6)
式中:psys為校準系統補償值,Pa;δp8為由連接件的溫差引起的影響量,Pa;δp9為泄漏引起的影響量,Pa; δp10為讀數穩定性引起的影響量,Pa。
所以,校準系統引起的標準不確定度為:
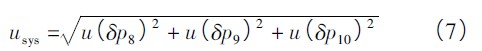
1.4、合成標準不確定度
由以上可知合成標準不確定度為:
![]()
1.5、擴展不確定度
取包含因子k = 2,擴展不確定度為:
U = kuc(k = 2)
2、實例分析
下面以一只測量范圍為1~100Pa 的熱傳導真計現場校準為例,計算其在10Pa 點的不確定度。其中,標準器示值為10. 213Pa, 系統補償值為0.001Pa,被測真空計示值為10.247Pa ( 表1 ~ 3 中均為參考值,應用時以實際示值為準) 。
表1 標準器引入不確定度計算匯總表
表2 被測真空計引入不確定度表
表3 標準系統引入的不確定度表
由表1 ~3 計算得ustd =1.09 × 10-2Pa,u uuc = 8.20 ×10-3Pa,usys = 1.30 × 10-2 Pa,其合成標準不確定度為:

3、結束語
通過以上分析可知,在真空計的現場校準過程中,由于條件復雜多變,要充分考慮各種不確定因素對校準結果帶來的影響,但往往由于影響因素過多我們無法全面估計,因此應當根據現場的實際情況做出恰當的評估和適當的篩選,可以忽略那些影響量過小或無法估計而又不至于對最終結果產生很大偏差的影響量,才能保證最終得到的校準結果在合理而有效的范圍之內。