差動式快開閥開閥過程動力學分析與仿真

2013-09-05 孫振華后勤工程學院軍事供油工程系

　　以電磁閥為先導閥，自力式差壓控制的快開閥用于模擬產生管線發生破裂時的瞬間泄露工況，在設計時間內快速、穩定的開啟是該閥研制的關鍵技術難點。分析了差動式快開閥的機構及開啟原理，以流體力學基本理論為基礎，建立了壓降隨開度變化的關系，完成了閥門開啟過程動力學分析與仿真計算，得到了不同閥門開度下的開啟時間、速度及加速度，閥芯運動過程中的驅動力逐漸減小，開啟時間、開啟速度及加速度三者隨開度的變化呈非線性變化關系。計算結果表明，閥體開閥時間與實驗實測數據吻合良好，開閥過程的速度及加速度與實驗結果一致，為工程設計中主要部件的優化研究提供了理論依據。

　　泄漏是管線常見的事故工況，管線泄漏不僅造成油料的損失，影響管線的正常輸送，甚至會導致管線輸送中斷，直接影響戰爭后勤油料保障;大量的油料泄漏還會造成嚴重的環境污染，危及人民的生命財產安全。因此，必須對管線使用和管理人員進行泄漏事故工況的針對性訓練，提高處置泄漏事故的能力。

　　為此，可設計研制一套訓練輔助裝置，模擬產生瞬間泄漏等事故工況。該裝置突發泄漏工況的模擬關鍵在于快開閥的研制。目前國內外高速開關電磁閥控制流量較小，單一依托電磁閥無法滿足該訓練輔助裝置控制需求。本文研究的快開閥采用電磁控制先導閥，主閥利用差壓控制原理，既可有效提高控制流量，其開啟響應時間也能滿足控制需求。由于該閥在輸油現場使用，不宜采用電氣原理，而應采用科學、穩定、可靠的液體與機械控制技術來實現高速開啟，其中閥體的開閥過程是研制該閥的關鍵性技術。本文重點介紹了差動式快開閥開閥過程的動力學原理、閥體結構和仿真計算，并對計算結果進行了分析和討論。

1、閥體結構與開閥過程動力學分析

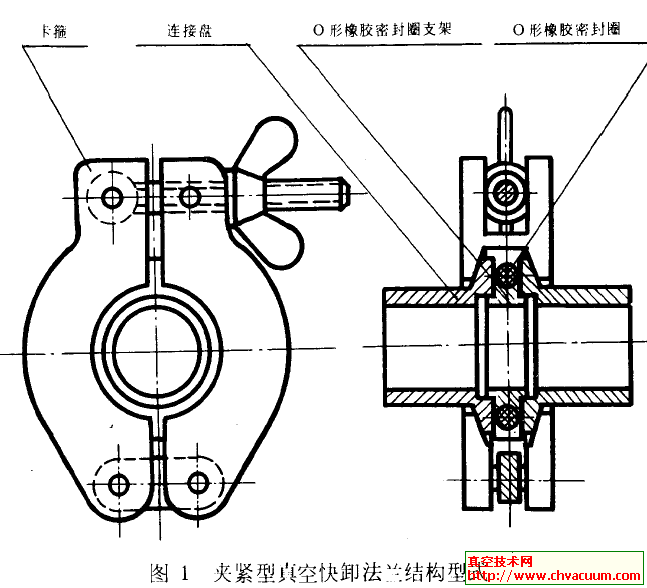
　　閥體結構如圖1所示。快開閥未動作時，電磁先導閥關閉，流體經孔1流入并充滿閥芯內部空腔，流體對閥芯底部壓力等于閥芯內部流體壓力，彈簧預壓力等于底座對閥芯的支持力，閥芯受力平衡。當電磁先導閥通電開啟，流體經孔2流出。由于孔2直徑遠大于孔1直徑，流體在閥芯內部無法聚壓，閥芯底部受力大于腔內流體壓力、彈簧力與流體粘性摩擦力的合力，使閥芯向上運動，閥門開啟，大部分流體從閥芯右側流出。閥門的開啟程度由限開度機構控制。

圖1 快開閥結構簡圖

圖2 閥內空腔劃分圖

2、閥體開閥時間計算

　　如圖2所示，閥內空腔直徑不同，為了便于分析，將閥內空腔(有流體流經的部分)分為a，1，2，3，4，5幾個部分，流體在每個部分流動都相當于在圓管內流動，只是長度和直徑有所區別。a部分流量、上下壓差、長度、直徑分別表示為Qa，ΔPa，La，da;1部分可表示為Q1，ΔP1，L1，d1，其他依次類推。

　　閥門在開啟過程中，空腔內的流體經孔2排出，腔3內流體排出時間即為閥門開啟時間。

　　2.1、閥芯內腔流量計算

　　主閥閥體是傾斜的，閥芯空腔內劃分的各個部分可看成為非水平管。非水平管道層流時，流體重力只影響位能，不影響流動特性。因此，在只討論速度分布的情況下，閥芯空腔內各個部分流體速度分布可按水平管處理，根據水平管的N-S方程，經進一步計算，水平管內過該截面的流量可表示為：

(1)

　　式中，d為水平管的直徑。

　　2.2、閥芯空腔各部分壓差計算

　　根據圓管流量式(1)得到閥空腔內6個部分的流量，分別為：

　　在閥芯向上運動的過程中，a，1，2部分的流體液面不會發生變化，認為流量沒有變化，即Qa=Q1=Q2。根據流量關系得：

　(2)

　　閥芯向上運動過程中，腔3內流體經孔2中排出，腔3內液位會有明顯變化;腔4，5內液位不會產生變化，直到閥門達到最大開度。若dt時間內，閥芯沿軸線方向上升dx，即腔3內有dx長度的流體流出，考慮到從腔2內進入的流量，可表示為：

　(3)

　　由于腔4，5內的凈剩流量沒有變化，則，Q3=Q4=Q5，由6個部分流量表達式及式(3)，可以得到下面關系式：

　　2.3、閥芯腔內壁面粘性摩擦力計算

　　閥門在開啟過程中，流體受擠壓經孔2中排出，閥芯內腔壁面會對流體產生一個阻礙其運動的力，這個力就是流體對閥芯內腔內壁面產生的粘性摩擦力。

　　根據牛頓內摩擦定律，可得管中流體產生的切應力為：

　　在管壁處τ=τ0，r=R=d/2，則有

　　于是流體對管壁的摩擦力可表示為：

　(4)

　　根據式(4)可以得到，流體對閥空腔內6個部分的摩擦力為：

　(5)

　　2.4、壓差力計算

　　為便于計算壓差產生的力，將閥芯內腔部分由軸線方向向兩側劃

　　幾個區域，區域劃分以此前劃分的6個部分的直徑大小(da　　經計算，各部分壓差力分別為：

　(6)

圖3 計算壓差力時閥內空腔劃分圖

　　2.5、閥門開啟時間分析

　　閥門在開啟過程中，彈簧受力壓縮，彈簧壓力f的大小可近似認為等于流體壓差力與流體對閥芯內壁面粘性摩擦力的合力，表示為：

　(7)

　　將式(5)、(6)代入式(7)，得：

　(8)

　　將式(2)代入式(8)，進一步化簡，得：

　　(9) 式中：

　　彈簧產生的壓力f可表示為：

　　式中：k表示彈簧的彈性系數;x表示主閥開度，即閥芯沿軸線上升的距離;

　　表示彈簧的預壓量。將上式代入式(9)，得：

　(10)

　　閥門在開啟過程中，a部分流速很大，壓差ΔPa比其他幾個部分的壓差大得多，可近似認為a部分的壓差ΔPa同閥芯上下壓差ΔP(閥內6個部分壓差之和)相等，故式(10)又可表示為：

　(11)

　　閥芯向上運動過程中，閥芯上、下的壓力差ΔP與主閥開度相關，可表示為ΔP=f(x)，其中，x為主閥開度，函數關系f需通過實驗測得。則式(11)可變化為：

　(12)

　(13)

　　對式(13)積分，得：

　　當x=0時，t=0，則

　　上式可進一步簡化，得閥門開啟時間為：

(14)

　　本文所研究的閥門跟截止閥原理相同，根據研究，閥門開啟時壓降與主閥開度之間的關系ΔP=f(x)滿足雙曲線變化關系，可設：

(15)

　　式中：P0為閥門開啟前主閥底部壓力，近似為管線運行壓力;A，B，C是閥門壓降與開度變化關系的系數，可通過實驗測得。

　　閥芯上、下的壓降隨開度變化關系可經實驗測得。在式(14)中代入不同的開度x值，可得不同開度情況下的閥門開啟時間。

　　2.6、分析結果

　　簡化閥門結構，并進行一定的假設，采用數值模擬的方法得到式(15)的系數值;式(14)中，除閥門開度x值外，其余都是已知數，代入不同的主閥開度x值，就可得到不同開度情況下的閥門開啟時間理論值。樣機實驗中，利用瞬變數據采集系統，通過位移傳感器，閥芯向上每運動2mm記錄一次時間數據，得到不同開度下閥門開啟時間實驗值。結果見表1。

表1 閥門開啟時間理論值、實驗值對比