調節閥振動問題在高參數汽輪機中普遍存在，已嚴重影響到機組運行的經濟性和安全性。調節閥振動為復雜的流固耦合，依靠數值模擬揭示由流體誘發振動的原因逐漸成為重要的手段，但是目前針對調節閥的大部分數值模擬并未考慮閥桿系統振動對閥內流場的影響。

　　調節閥振動問題在高參數汽輪機中普遍存在，已嚴重影響到機組運行的經濟性和安全性。調節閥振動為復雜的流固耦合，依靠數值模擬揭示由流體誘發振動的原因逐漸成為重要的手段，但是目前針對調節閥的大部分數值模擬并未考慮閥桿系統振動對閥內流場的影響。該文在數值模擬中利用Fluent中動網格模塊和UDF函數，對比分析了閥碟在靜止和不同振幅、振動頻率下對閥內流場的影響。在網格變形中使用了一種新穎的網格控制方法，即固定閥碟邊界層網格使網格在較大尺度區域變形，確保了數值計算準確、順利的進行。數值計算結果表明當閥碟頂端振幅小于0.6mm時，閥碟上壓力呈現隨機波動;當閥碟頂端振幅為1mm時，閥碟上壓力隨閥碟移動出現明顯的周期性波動，此時數值模擬應考慮閥桿系統振動的影響。隨著振動頻率的增加，閥碟上周期性的壓力波動逐漸滯后于閥碟移動，當頻率達到193.6Hz時周期性波動消失。

　　調節閥位于主蒸汽管道和汽輪機之間，是控制機組功率的重要通流部件。隨著機組單機容量增加和蒸汽參數的提高，汽輪機調節閥常處于極其嚴酷的工況環境中，由流體誘發調節閥的振動所產生的事故屢見不鮮，已成為威脅電廠安全運行的重要因素。隨著CFD的不斷發展和完善，數值計算因其方便性和可視化等優點受到了眾多學者青睞，在分析流體誘發的調節閥振動中扮演越來越重要的角色。但真空技術網(http://smsksx.com/)認為由于調節閥振動是一種復雜的三維流固耦合現象，到目前為止對于該問題的機理始終沒有明確的論斷。

　　Araki認為當調節閥中閥桿系統的振動在小開度時為一階縱向高頻振動，在開度逐漸增大后主要為一階彎曲振動。Zhang通過二維定常數值模擬指出閥內不對稱流是引起振動的主因。Morita的三維非定常數值模擬進一步表明閥碟下方高壓區的周向移動導致了閥桿系統的振動。Morita還通過實驗研究了閥桿在弱連接下的壓力波動和振動的關系，指出在中等升程時壓力波動和閥固有頻率之間存在鎖定現象，在鎖定區域阻尼比接近于零且振幅較大，而在非鎖定區域阻尼比大于5%。Tecza通過有限元法確定了閥桿系統的固有頻率，并指出閥碟最有可能的運動為傾斜和擺動，并按照閥桿擺動頻率550Hz最大擺動角度為±0.02°進行了瞬態力響應分析。Yonezawa的研究表明閥碟在靈活狀態下的壓力波動高于閥碟緊固時的波動，將閥桿系統的振動分為振動幅值較小時的強迫振動和振動幅值較大時的自激振動。國內關于調節閥的數值計算研究往往不考慮閥桿系統振動的影響，用數值模擬分析調節閥的閥型對振動、流量、壓損、流型等因素的影響，而在調節閥快關和開啟特性中不得不考慮閥碟移動，利用動網格計算閥內的瞬時流場的變化。但是在計算過程中由于網格畸變過大而導致計算發散一直是困擾數值計算能否順利進行的關鍵因素。通過增加網格尺度減小網格畸變往往收效甚微，甚至有時還會因網格尺度過大而影響計算準確性。

　　從這些研究可以看出，以往借助CFD分析閥內的流型及流體誘發的調節閥閥桿系統振動大都忽略振動對閥內流場的影響。但當振動幅值較大時，必然會對內部流場的產生影響。本文針對以上問題，利用Fluent中的彈簧光順模型和UDF函數，對比分析了某600MW模化調節閥的閥碟頂端振幅分別為0.6mm、1mm，及振動頻率分別為46.4、92.8、185.6Hz時閥桿系統振動對閥內流場的影響。計算中提出的保護邊界層的網格變化方法和數值計算結果為后續數值計算中網格控制和是否考慮閥桿系統振動對閥內流場的影響提供了重要的參考。

1、數值計算的物理模型

　　根據相似原理對某電廠600MW調節閥進行了模化實驗，圖1為模化后調節閥沿進口方向中心截面示意圖。閥桿和閥碟所組成的系統可看做為以提升機構與閥桿連接處為固定點，頂端帶有集中質量的長細粱結構[3]。由于調節閥在中等升程下，閥碟上壓力波動呈現以低頻占優的寬頻激勵特性，所以主要考慮閥桿閥碟所組成系統的一階彎曲模態對閥內流場的影響。利用Workbench計算此調節閥閥桿系統固有頻率，結果表明此調節閥閥桿系統一階彎矩的固有頻率為46.4Hz。為對比閥桿系統按照一階彎矩振動在不同振動頻率下對閥內流場的影響，計算了頻率分別為一階彎矩頻率及2倍、4倍一階彎矩頻率(即頻率分別為：46.4、92.8和185.6Hz)這3種方案。為對比不同幅值對閥內流場的影響，計算了閥碟固定、閥碟頂端振動幅值為0.6和1mm這3種方案。以上計算中，閥桿系統振動方向為沿圖1中進口中心截面。為后續分析方便，定義三維坐標所指方向如下：x軸正方向所指的沿來流方向為東側用E表示，x軸負方向所指為西側用W表示;y軸所指方向沿閥桿軸向;z軸所指方向垂直于沿來流中心截面，如圖1、2所示。

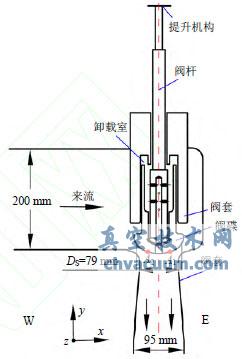
圖1 調節閥結構圖

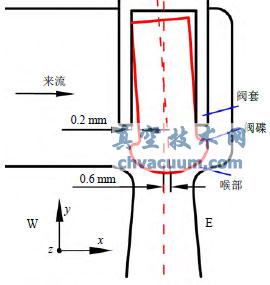
圖2 閥碟偏向西側示意圖(h=0.6mm)

　　圖2為閥碟頂端最大振幅h=0.6mm時的閥碟偏向東側示意圖，可以看出閥碟可能出現的最大振幅主要由閥碟和閥碟套間隙0.2mm決定。隨著使用時間增加，閥碟表面的涂層不斷脫落此間隙可達到0.4mm，此時閥碟頂端振幅為h=1mm。由于卸載室內流過的流量占主流流量小于1%，對主流的影響可忽略不計，因此在動網格計算中不考慮由卸載室流過的流體。

2、數值計算方法和動網格設置

　　本文湍流模型采用Fluent中基于realizablek-ε的兩方程的DES模型。DES方法結合了雷諾平均與大渦模擬技術的優點，在近壁面的附面層內采用RANS方法，用realizablek-ε兩方程模型模擬其中的小尺度脈動運動;在遠離物面區域將湍流模型耗散項中的湍流尺度參數用網格尺度與一常數的乘積代替，使其起Smagorinski大渦模擬的亞格子雷諾應力模型的作用。這樣既能在附面層內發揮前者計算量小的優點，又可以在遠離物面的區域對大尺度分離湍流流動進行較好的模擬。

　　選取實際運行和模化實驗中閥桿系統振動較大的工況，即相對升程(調節閥的絕對升程與配合直徑比值)εL=11%，壓比(調節閥出口靜壓與進口總壓的比值)ψP=0.8作為計算工況。進口設為總壓P0=123.5kPa，溫度為298K。出口設為靜壓，其值P2=98.8kPa，溫度為295K，所選取數據均為模化實驗所測。

　　結合Fluent中UDF函數和彈簧光順模型可實現閥碟在東西截面上以不同振幅和頻率按正弦振動。UDF函數中主要通過式(1)控制振動。

cg_omega=Acos(BTime) (1)

　　式中：cg_omega為在xy平面內轉動角速度，參數B控制頻率，A控制振動幅值。Fluent中彈簧光順法把網格的邊理想化為節點間相互連接的彈簧，網格移動前彈簧組成的系統處于平衡狀態。在網格邊界節點發生位移后，會產生與位移成比例的力，從而由力轉化出網格節點移動的距離。彈簧光順方法并不將網格質量作為網格更新的判斷因素，而只是單純的將邊界運動作為參數擴散至計算域中，因此無需插值，網格拓撲始終不變。

　　網格在ICEM中生成且全都為六面體結構化網格，總體網格數為800萬。網格未發生移動時，在ICEM中網格質量2項評價標準如下：Determinant2´2´2>0.6，網格角度Angle>18°。使用Fluent計算時，當網格質量Determinant2´2´2>0.2且網格角度Angle>9°就可以確保數值計算順利進行，由此可見初始時網格質量非常高。為保證閥出口為均勻流和避免回流的產生，將閥出口加長到出口直徑的10倍，加密了喉部和閥碟下方流動變化較為劇烈的區域網格，保證在此區域內網格均勻變化和邊界層內y+<=5。

　　圖3為沿東西方向中心截面網格和網格變形后的局部示意圖。由圖3可以看出，在閥座喉部區域網格很密，閥碟周圍第一層網格厚度為0.004mm。若不加以特殊處理，閥碟移動極易使邊界層網格畸變過大而使計算發散。考慮到邊界層內流動對流場的巨大影響，同時為保護閥碟處邊界層網格，將包圍閥碟部分區域網格設置為剛體區，即在計算中這部分網格不會變形。而此區域外的網格設置為變形區，即在閥碟移動中這部分網格會產生相應的變形，剛體區域和變形區域的劃分如圖3所示。通過控制彈簧光順法中兩個參數：彈簧常數因子與邊界節點松弛因子，將網格中較大的變形控制在變形區域中靠近剛體區外圍，而保證靠近閥座處較密的網格基本不變。由圖3可以看出，當閥碟頂端偏向東側1mm后喉部網格并沒有發生畸變。將閥碟頂端偏向東側1mm的網格重新導入ICEM中，其網格質量為：Determinant2´2´2>0.25，網格角度Angle>10°，足以滿足Fluent計算中對網格的要求動網格常用于調節閥在開啟或關閉計算中，此時由于閥碟位移較大使得網格變形量增大，為保證網格在大變形后畸變率低不得已采取較粗的網格，邊界層網格通常難以嚴格滿足湍流模型的需求。在中小升程下調節閥內流動往往為復雜的三維超音速流動，粗網格通常難以精確的捕捉激波、射流分離和邊界層內的諸多流動細節，因此所得的結果往往只能定性的分析閥內的流動情況。本文在數值計算中所采用DES湍流模型雖對流過復雜機構的高雷諾數分離流具有非常高的預測能力，但是DES湍流模型高度的依賴網格尺度、網格質量和邊界層內的網格布置。針對閥碟小幅振動特性，借助Fluent中彈簧光順模型，創新性的將邊界層網格剛體化，將閥碟移動造成的網格變形“轉移”到相對尺寸較大的區域，既實現了800萬結構網格網格變形也滿足了湍流模型對網格的需求。

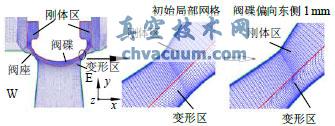
圖3 沿東西方向中心截面初始網格和局部網格變形圖

3、數值計算結果

　　在閥碟下表面沿振動的方向上設置了兩個監測點A1和A2，其位置如圖1中所示。圖4為閥碟靜止狀態下，閥碟上兩測點隨時間的壓力變化時域圖，可以看出兩測點處的壓力呈現無規則的波動狀態。圖5和圖6是閥桿系統以頻率f=46.4Hz振動閥碟頂端振幅分別為h=0.6mm和h=1mm時的閥碟上2個測點壓力波動時域圖，2圖中右側同時標明了閥碟位移方向。由圖5可以看出當閥碟頂端振幅為0.6mm時，閥碟上壓力測點波動仍呈現隨機狀態，并未受到閥碟運動的影響。而由圖6可以看出，當閥碟頂端振幅為1mm時，閥碟監測點壓力明顯出現了隨閥碟位移變化的周期性波動現象。當閥碟運動到東側時，位于東側的監測點A1的波動明顯增大;當閥碟運動到西側時，位于西側的監測點A2的波動明顯增大。

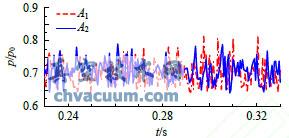
圖4 兩監測點壓力波動時域圖(閥碟固定)

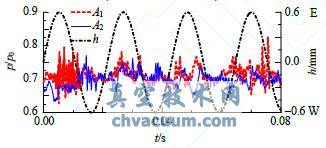
圖5 兩監測點壓力波動時域圖(h=0.6mm，f=46.4Hz)

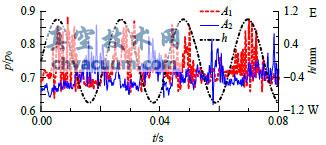
圖6 兩監測點壓力波動時域圖(h=1mm，f=46.4Hz)

　　圖7為在計算中調節閥沿進口方向中心截面上三種典型的流型。可以看出從兩側喉部流出的高速射流在閥碟下方區域某點撞擊后向出口流動。跨音速撞擊射流自身的不穩定性使得喉部以后的射流處于不斷的擺動狀態，撞擊點也在閥碟下方不斷移動。當由撞擊形成的高壓區移動到監測點附近時就會導致監測點處壓力脈動增加。當閥碟處于靜止狀態時，由兩側喉部流出的高速射流的強度相當，高速射流在閥碟下方撞擊后不會出現射流角度發生較大偏斜的流型，撞擊位置相對遠離閥碟下方，所以閥碟監測點處不會出現明顯的壓力波動。而當閥碟在振動中偏向一側時(如圖2中閥碟偏向東側為例)，由西側較寬的喉部處有更多的流體流過，此時由西側喉部流出的流體具有更多的能量推動由東側喉部流出的高速射流偏向東側，撞擊點也會更接近監測點A1處，導致A1處壓力波動增大。同樣當閥碟偏向西側時，高速射流撞擊點位置也會轉移到A2附近，所以A2的壓力波動也會相應增加。

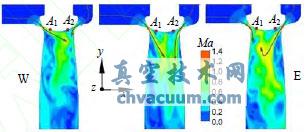
圖7 調節閥沿進口中心面Ma圖

　　由圖4—6可以看出，當閥碟頂端的振幅小于等于0.6mm時，數值模擬此調節閥內流動可以不考慮閥桿系統振動對流場的影響。但當閥碟頂端振幅達到1mm時，閥內的流動明顯受到閥桿系統振動的影響，此時須對其加以考慮。閥碟頂端振幅主要由閥碟和閥碟套間隙決定，當這一間隙足夠大時，閥桿系統的振動就會引起調節閥內流場周期性波動，形成流固耦合振動，這種振動往往嚴重威脅調節閥的安全。

　　圖8和圖9為閥碟頂端振幅為h=1mm，振動頻率分別為f=92.8Hz和f=185.6Hz時的閥碟兩測點壓力波動時域圖。當閥桿系統按照92.8Hz振動時，兩測點壓力脈動仍隨閥碟位移有明顯的周期變化，但壓力波動已出現了滯后現象。當按照185.6Hz振動時，閥碟測點處雖出現了較大幅度的壓力脈動，但和位移已沒有明顯的周期對應關系。這是由于兩側高速射流的擺動存在慣性，隨著振動頻率的增加兩側射流難以及時跟隨閥碟一起運動，所以在監測點處也不會呈現明顯的隨閥碟移動的壓力波動。

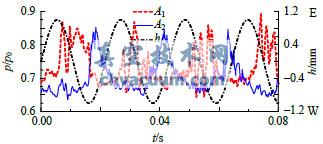
圖8 兩監測點壓力波動時域圖(h=1mm，f=92.8Hz)

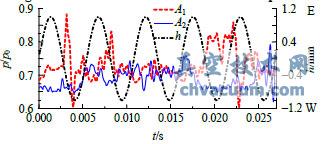
圖9 兩監測點壓力波動時域圖(h=1mm，f=185.6Hz)

4、結論

　　本文利用FLUNT中動網格模型和UDF函數，考慮了閥碟在不同振動幅值和振動頻率下對閥內流場的影響，得到如下結論：

　　1)在動網格變形中，采取固定閥碟邊界層處附近的網格使網格在尺度相對較大的位置移動變形。避免了以往動網格變形中由于邊界層網格畸變過大而導致的計算發散。這種高質量的網格變化方法對調節閥內利用動網格模擬閥碟移動對閥內流場的影響有重要意義。

　　2)動網格計算表明當閥碟頂端振動幅值小于等于0.6mm時，閥碟上壓力波動為隨機波動;當閥碟頂端振動幅值達到1mm時，閥碟上壓力波動呈現隨閥碟位移周期性變化的特點，此時數值計算中應考慮到閥桿系統振動對流場的影響。

　　3)隨著閥桿系統振動頻率的增加，由于主流流型變化存在慣性，閥碟上的壓力波動隨閥碟位移出現滯后現象直至周期性波動消失。數值模擬了閥桿系統按照不同振幅和振動頻率對閥內流場的影響，對后續數值模擬中是否考慮振動對閥內流場的影響提供了參考。