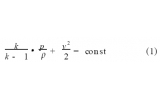針對(duì)目前使用的射流式真空發(fā)生器耗氣量大的局限性，提出了一種帶可調(diào)錐的流量自調(diào)式射流真空發(fā)生器的新結(jié)構(gòu)。為了解決該真空發(fā)生器在減少耗氣量與維持真空度之間的矛盾，以尋求最佳的流量調(diào)節(jié)方案，需要對(duì)調(diào)節(jié)過程的二維流場(chǎng)和可調(diào)錐的受力進(jìn)行高精度的分析。為此對(duì)該型真空發(fā)生器內(nèi)部超音速流場(chǎng)進(jìn)行了數(shù)值模擬，分析了可調(diào)錐的不同工況對(duì)流道內(nèi)流場(chǎng)中壓力和馬赫數(shù)分布的影響規(guī)律。結(jié)果表明，隨著可調(diào)錐進(jìn)入真空噴管喉部距離x的增大，可調(diào)錐對(duì)真空噴管內(nèi)的流場(chǎng)擾動(dòng)加劇，真空發(fā)生器的引射能力減弱。因此，為了保證正常工作所需的真空度并達(dá)到最大的節(jié)能效果，應(yīng)將可調(diào)錐進(jìn)入真空噴管喉部的距離控制在一定的范圍內(nèi)。分析表明，如果可調(diào)錐進(jìn)入噴管喉部的距離不超過2mm，則可使最低真空度大于65kPa，并能減少30%的耗氣量。

1、引言

　　真空發(fā)生器作為一種局部真空發(fā)生裝置以其結(jié)構(gòu)簡(jiǎn)單、工作可靠、使用方便等優(yōu)點(diǎn)得到了廣泛的應(yīng)用。但是，由于目前使用的射流式真空發(fā)生器在工作時(shí)必須持續(xù)定量供氣，空氣消耗量很大，相應(yīng)耗能也大。因此，如何解決真空發(fā)生器在使用中耗能大的問題，同時(shí)又要達(dá)到其原有的工作性能指標(biāo)，是真空發(fā)生器研制中需要解決的一項(xiàng)技術(shù)難題。

　　為此，我們提出了一種流量自調(diào)式射流真空發(fā)生器的總體技術(shù)方案，并申請(qǐng)了國家發(fā)明專利(專利申請(qǐng)?zhí)?00610040832.1)。該技術(shù)方案中，在拉瓦爾真空噴管前方設(shè)置了可調(diào)錐，在真空產(chǎn)生階段，可調(diào)錐離噴管喉部具有一定距離，對(duì)真空噴管的通流面積沒有影響，真空發(fā)生器可以快速響應(yīng)建立設(shè)定的真空度；在真空維持階段，通過控制可調(diào)錐進(jìn)入噴管喉部的距離可實(shí)現(xiàn)對(duì)真空發(fā)生器供氣流量的調(diào)節(jié)。前期的試驗(yàn)研究已經(jīng)初步證實(shí)了該技術(shù)方案的有效性，當(dāng)可調(diào)錐進(jìn)行調(diào)節(jié)時(shí)，可以減少供氣流量。但同時(shí)也發(fā)現(xiàn)，此時(shí)真空發(fā)生器的維持真空度也會(huì)有所下降。所以，為了保證該真空發(fā)生器能夠維持正常工作所需真空度，同時(shí)也能達(dá)到最大的節(jié)能效果，需要確定合理的可調(diào)錐調(diào)節(jié)策略，這就需要對(duì)可調(diào)錐的調(diào)節(jié)過程及可調(diào)錐的受力進(jìn)行精確的分析。實(shí)際上，該型真空發(fā)生器噴嘴喉部的形狀和面積是變化的，流動(dòng)過程涉及亞聲速和超聲速兩個(gè)階段，此外，在變截面情況下其流動(dòng)是二維的，比較復(fù)雜。所以，采用傳統(tǒng)的一維集中模型分析方法無法給出真空發(fā)生器內(nèi)部流體流動(dòng)精確的速度分布、壓力分布、能量損失等信息，因而也就無法對(duì)可調(diào)錐部件進(jìn)行正確的設(shè)計(jì)和控制，這是該型真空發(fā)生器研制中面臨的一個(gè)難題。所以，進(jìn)行流量自調(diào)式真空發(fā)生器內(nèi)部流場(chǎng)精確的數(shù)值分析，對(duì)該型真空發(fā)生器的結(jié)構(gòu)設(shè)計(jì)及可調(diào)錐的合理調(diào)節(jié)是十分必要的。

2、采用可調(diào)錐的流量調(diào)節(jié)原理

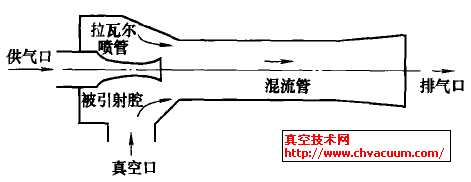
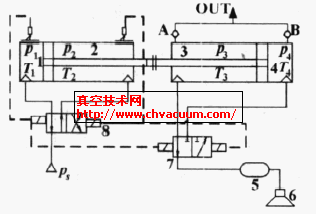
　　普通的射流式真空發(fā)生器主要由先收縮后擴(kuò)張的拉瓦爾噴管、被引射腔和混流管等組成，如圖1a所示。當(dāng)供氣壓力與噴管喉部壓力的比值大于一定值時(shí)，供給氣體在拉瓦爾噴管中加速形成超聲速射流，引射流體在超聲速射流的剪切作用下被卷吸至混合腔，而后形成單一均勻的混合流體，經(jīng)過第二喉管和擴(kuò)散腔減速壓縮到一定的背壓后排出真空發(fā)生器。在混合的過程中，由于激波系和邊界層不斷地進(jìn)行相互作用，從而形成了極為復(fù)雜的流動(dòng)結(jié)構(gòu)，再加上粘性干擾等物理現(xiàn)象使得對(duì)真空發(fā)生器內(nèi)部氣體流動(dòng)狀態(tài)的理論描述變得十分復(fù)雜。

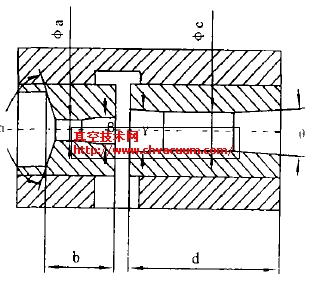
　　我們所提出的采用可調(diào)錐的流量自調(diào)式真空發(fā)生器的流量調(diào)節(jié)原理如圖1b所示。在真空發(fā)生器拉瓦爾噴管的前方設(shè)置一個(gè)與其同軸的可調(diào)錐，當(dāng)真空發(fā)生器的工作真空度達(dá)到一定值時(shí)，調(diào)節(jié)可調(diào)錐沿軸向方向的位移，改變真空噴管喉部的有效流通面積，從而減小真空發(fā)生器的供氣流量，達(dá)到節(jié)能的目的。詳細(xì)的調(diào)節(jié)原理請(qǐng)參見文獻(xiàn)。

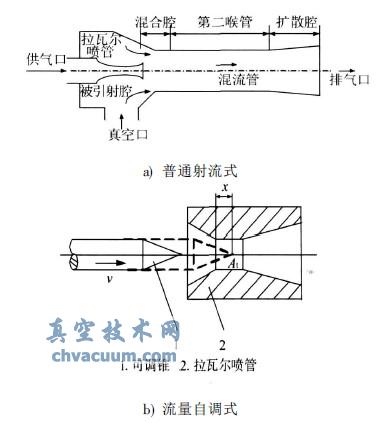
圖1 真空發(fā)生器工作原理示意

3、變截面二維流場(chǎng)的數(shù)值模擬研究

　　考慮真空發(fā)生器被引射腔入口截面處引射流體的速度與工作流體相比很小，因此將圖1a中被引射腔的側(cè)向入口簡(jiǎn)化成軸向環(huán)形入口，這樣便可將真空發(fā)生器內(nèi)部氣流管道簡(jiǎn)化為沿軸線的變截面圓管道，并假設(shè)流場(chǎng)具有軸對(duì)稱性，所以可將流場(chǎng)計(jì)算域簡(jiǎn)化成二維的軸對(duì)稱模型。數(shù)值模擬結(jié)果表明，這種簡(jiǎn)化所帶來的計(jì)算差值非常小，但計(jì)算量大大減少。

　　3.1、控制方程

　　非定常可壓縮的射流滿足如下的Navier-Stokes方程：

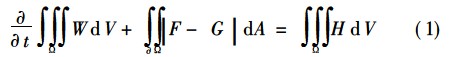
　　其中，8為控制體，98為控制體邊界，W為求解變量，F(xiàn)為無粘通量，G為粘性通量，H為源項(xiàng)。

　　式中Q——流體的當(dāng)?shù)孛芏龋琸g/m3；u、v、w——流體的速度分量，m/s；E——單位體積總能量，J；p——流體壓力，Pa

　　3.2、計(jì)算模型及網(wǎng)格劃分

　　模擬研究中使用的部分參數(shù)是：可調(diào)錐錐頂角A=2arctan(1/4)，可調(diào)錐錐面在軸向方向的投影長(zhǎng)度為4mm，拉瓦爾噴管喉部直徑為2mm，真空噴管入口錐角為100b，第二喉管直徑為5.2mm。圖2給出了真空發(fā)生器的計(jì)算模型網(wǎng)格劃分，為了便于顯示，圖中只給出了實(shí)際計(jì)算網(wǎng)格密度的20%。網(wǎng)格劃分采用分塊結(jié)構(gòu)化網(wǎng)格，為捕捉激波和邊界層，在真空噴管的出口及工作氣體與引射氣體的混合面上進(jìn)行了適當(dāng)?shù)募用堋６�維模擬計(jì)算模型的中心邊界為對(duì)稱軸，各變量在對(duì)稱軸法線方向的梯度及垂直于對(duì)稱軸的速度為零。

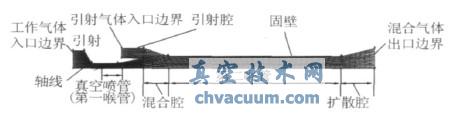
圖2 真空發(fā)生器內(nèi)部流道的網(wǎng)格劃分

　　采用二階精度的有限體積法離散控制方程，采用標(biāo)準(zhǔn)k-E湍流模型，近壁面處使用壁面函數(shù)修正的方法對(duì)真空發(fā)生器的超音速混合過程進(jìn)行數(shù)值模擬。時(shí)間離散采用多重Runge-kutta顯式格式迭代，并采用多重網(wǎng)格方法加速迭代收斂、自適應(yīng)網(wǎng)格方法捕捉激波，以期獲得與網(wǎng)格無關(guān)的解。

　　工作氣體和引射氣體入口邊界均采用壓力入口邊界，給定滯止壓力、滯止溫度和湍流條件；混合流體的出口邊界采用壓力出口邊界，給定靜壓及回流條件；固體壁面采用無滑移、無滲流、絕熱邊界。

　　3.3、模擬結(jié)果分析

　　3.3.1、可調(diào)錐調(diào)節(jié)距離對(duì)流場(chǎng)的影響

　　設(shè)可調(diào)錐進(jìn)入真空噴管喉部的距離用x表示(如圖1b所示)。分別對(duì)無可調(diào)錐時(shí)以及x=0、x=0.5mm、x=1.0mm、x=1.5mm、x=2.0mm、x=2.5mm等7種情況進(jìn)行了分析計(jì)算。為簡(jiǎn)便起見，圖3中a)~d)只列出了無可調(diào)錐、x=0、x=1.0mm、x=2.0mm等幾種條件下對(duì)應(yīng)的馬赫數(shù)分布圖。

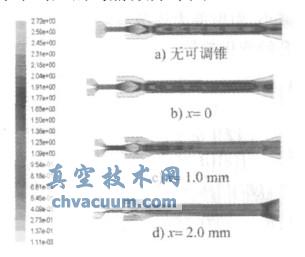
圖3 流動(dòng)馬赫數(shù)分布圖

　　圖4給出了無可調(diào)錐以及有可調(diào)錐(x=0)兩種條件下的馬赫數(shù)分布曲線和沿軸線的靜壓力分布曲線對(duì)比。從圖4中可以看出，對(duì)應(yīng)x=0的情況，可調(diào)錐的存在對(duì)真空發(fā)生器內(nèi)氣體流動(dòng)的影響是使真空噴管喉部初始段的流場(chǎng)產(chǎn)生了一些微小的擾動(dòng)，使馬赫數(shù)略微增大，靜壓力略微減小，并伴隨有微小值的波動(dòng)。但是這種小擾動(dòng)很快就被衰減并消失，所以并沒有影響到混合腔及第二喉管中的流場(chǎng)結(jié)構(gòu)，兩種計(jì)算情況下流場(chǎng)的流動(dòng)馬赫數(shù)分布和沿軸線的靜壓力分布基本相同。這說明在可調(diào)錐未進(jìn)入真空噴管喉部前，可調(diào)錐的存在基本上不會(huì)對(duì)真空發(fā)生器的內(nèi)部流場(chǎng)產(chǎn)生影響，因此不會(huì)影響真空發(fā)生器的工作性能。

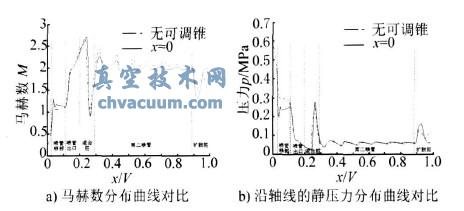
圖4 有、無可調(diào)錐時(shí)真空發(fā)生器內(nèi)部流場(chǎng)的對(duì)比

　　圖5給出了從x=0變化到x=2.5mm幾種計(jì)算條件下真空發(fā)生器內(nèi)部流場(chǎng)的馬赫數(shù)分布曲線和沿軸線的靜壓力分布曲線。結(jié)合圖3和圖5可以看出，隨著可調(diào)錐進(jìn)入真空噴管喉部的距離x的增大，真空噴管喉部?jī)?nèi)的馬赫數(shù)增大，超音速區(qū)域提前，且超音速區(qū)域內(nèi)的馬赫數(shù)值的振蕩也在加劇，說明可調(diào)錐對(duì)真空噴管喉部流場(chǎng)的擾動(dòng)加劇。同時(shí)，混合腔內(nèi)的超音速馬赫錐(射流核心區(qū)域)的長(zhǎng)度隨x的增大不斷減小直至完全消失，極限真空區(qū)由混合腔向拉瓦爾噴管漸擴(kuò)出口段內(nèi)移動(dòng)，混合腔內(nèi)的真空度水平下降。另一方面，隨著x值的增大，第二喉管中的馬赫數(shù)水平也在不斷減小，引射能力逐漸減弱，第二喉管內(nèi)的絕對(duì)壓力呈上升的變化趨勢(shì)。

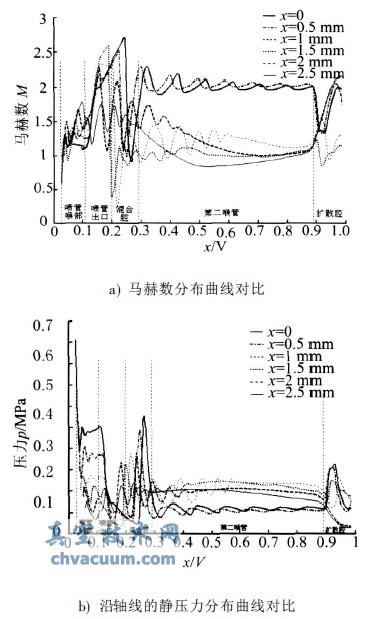
圖5 可調(diào)錐不同位置下的流場(chǎng)對(duì)比

　　在所計(jì)算的幾種情況中，當(dāng)x[210mm時(shí)，第二喉管中的馬赫數(shù)都大于(或等于)1，說明在這些計(jì)算條件下第二喉管仍能保持超音速(或音速)流動(dòng)；在x=210mm的計(jì)算條件下，混合腔內(nèi)的極限真空度仍可達(dá)到65kPa。當(dāng)x=2.5mm時(shí)，在第二喉管中馬赫數(shù)小于1，壓力高于0.1MPa，說明該區(qū)域內(nèi)的流動(dòng)已經(jīng)減速為亞音速流動(dòng)，而混合腔內(nèi)的真空度已減小到40kPa，說明此時(shí)真空發(fā)生器抽取真空的能力已經(jīng)很弱，已無法滿足真空系統(tǒng)正常工作的需要。

　　3.3.2、流場(chǎng)中流動(dòng)氣體對(duì)可調(diào)錐的作用力

　　由于可調(diào)錐與真空發(fā)生器的內(nèi)部流道同軸，且內(nèi)部流道中流場(chǎng)具有軸對(duì)稱性，因此，當(dāng)具有一定壓力的流動(dòng)氣體繞過可調(diào)錐時(shí)，流動(dòng)氣體作用在可調(diào)錐上的氣壓力徑向分力相互抵消。忽略氣體流動(dòng)時(shí)的重力和粘性摩擦力對(duì)可調(diào)錐的作用，則可調(diào)錐受氣壓力的作用如圖6所示。設(shè)工作氣體在可調(diào)錐左端面上的氣壓力為ps，在右側(cè)錐形壁面上的氣壓力分布函數(shù)為pi，則可調(diào)錐位于氣體流動(dòng)流場(chǎng)中所受到的氣壓力合力可表示為：

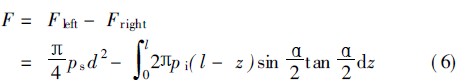
　　式中Fleft——作用在可調(diào)錐左端面上的氣壓力合力，N；Fright——作用在可調(diào)錐錐面上的氣壓力合力，N；ps——可調(diào)錐左端面的氣壓力，Pa；pi——可調(diào)錐錐形壁面上的氣壓力，Pa；d——可調(diào)錐圓柱段的直徑，mm；l——可調(diào)錐錐面在軸向的投影長(zhǎng)度，mm；A——可調(diào)錐錐頂角，A=2arctand2l

　　圖7a給出了對(duì)應(yīng)可調(diào)錐進(jìn)入真空噴管喉部不同距離x時(shí)計(jì)算得到的可調(diào)錐錐形壁面上的氣壓力分布pi。圖中橫坐標(biāo)的設(shè)置如圖6所示，坐標(biāo)零點(diǎn)為可調(diào)錐圓柱面和圓錐面的交截面與軸線的交點(diǎn)，向右為z軸正向。從圖7中可以看出，隨著x的增大，可調(diào)錐錐形壁面上的較高壓力區(qū)長(zhǎng)度逐漸減小，較低壓力區(qū)長(zhǎng)度變長(zhǎng)，且由高壓區(qū)向低壓區(qū)變化時(shí)的梯度增大。圖7b給出了對(duì)應(yīng)不同x值下的流動(dòng)氣體對(duì)可調(diào)錐的氣壓力合力F。可以看出，隨著x的增大，可調(diào)錐上受到的向右的正向合力逐漸增大，說明氣壓力有推動(dòng)可調(diào)錐向喉部運(yùn)動(dòng)的作用。

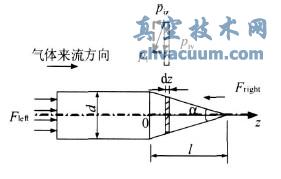
圖6 流動(dòng)氣體對(duì)流場(chǎng)中可調(diào)錐的作用力

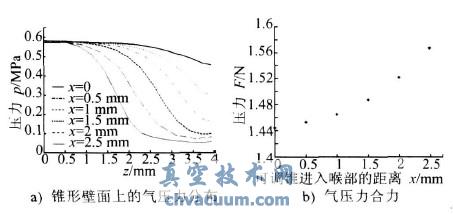
圖7 可調(diào)錐不同位置時(shí)的氣壓力分布和氣壓力合力

　　3.4、試驗(yàn)驗(yàn)證

　　試驗(yàn)測(cè)量了可調(diào)錐進(jìn)入真空噴管喉部不同距離時(shí)的真空度和供給流量。圖8a給出了真空度的試驗(yàn)與計(jì)算結(jié)果對(duì)比。可以看出，試驗(yàn)和計(jì)算得到的真空度具有相同的變化趨勢(shì)，隨著x值的增大，真空發(fā)生器所能達(dá)到的極限真空度逐漸減小，并且以x=2.0mm為拐點(diǎn)，在拐點(diǎn)之前，下降斜率較小，在拐點(diǎn)之后，下降斜率急劇增大。

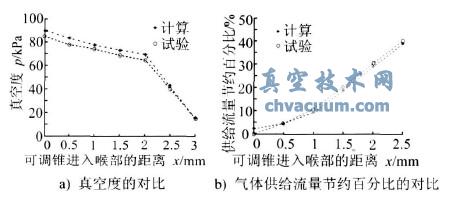
圖8 試驗(yàn)驗(yàn)證

　　試驗(yàn)中，當(dāng)x=2.0mm時(shí)，真空度仍可達(dá)到69kPa；當(dāng)x=2.5mm時(shí)，真空度值急劇下降，為43kPa；當(dāng)x=3.0mm時(shí)，真空度僅為16kPa，基本上喪失了真空抽取的能力。若以真空發(fā)生器的極限真空度不能低于65kPa為衡量真空發(fā)生器能否正常工作的標(biāo)準(zhǔn)，可以認(rèn)為可調(diào)錐進(jìn)入噴管喉部的距離不應(yīng)超過2.0mm，這與計(jì)算的結(jié)果是一致的。定義一個(gè)表示供給流量節(jié)約程度的百分?jǐn)?shù)為：

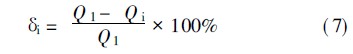
　　式中Q1——無可調(diào)錐時(shí)真空發(fā)生器的氣體供給流量，kg/s；Qi——對(duì)應(yīng)不同x值的氣體供給流量，kg/s；

　　圖8b給出了不同x值條件下供給流量節(jié)約百分比的試驗(yàn)和模擬計(jì)算結(jié)果的對(duì)比。可以看出，試驗(yàn)和計(jì)算結(jié)果基本一致，且x值越大，節(jié)約的供給流量百分比越大，說明節(jié)能效果越好，但結(jié)合圖8a可知，此時(shí)所能產(chǎn)生的真空度水平也會(huì)越低。因此，在確定流量自調(diào)式真空發(fā)生器可調(diào)錐的實(shí)際調(diào)節(jié)策略時(shí)，應(yīng)對(duì)供給流量和真空度兩個(gè)方面進(jìn)行綜合考慮。例如，若以真空發(fā)生器的極限真空度不能低于65kPa為衡量真空發(fā)生器能否正常工作的標(biāo)準(zhǔn)，則對(duì)應(yīng)本研究中所使用的流量自調(diào)式真空發(fā)生器來說，可以認(rèn)為可調(diào)錐進(jìn)入噴管喉部的距離不應(yīng)超過2.0mm，此時(shí)供給流量可節(jié)約近30%。

4、結(jié)論

　　為了尋求流量自調(diào)式射流真空發(fā)生器中可調(diào)錐的最佳調(diào)節(jié)方案，使該真空發(fā)生器真空維持階段在保證正常工作所需真空度的要求下達(dá)到最好的節(jié)能效果，對(duì)流量自調(diào)式真空發(fā)生器內(nèi)部的超音速流場(chǎng)進(jìn)行了數(shù)值模擬和試驗(yàn)研究，得到了以下的結(jié)論：

　　(1)分析了可調(diào)錐不同工況下流量自調(diào)式真空發(fā)生器內(nèi)部流場(chǎng)的壓力和速度分布，分析表明當(dāng)可調(diào)錐未進(jìn)入噴管喉部之前，可調(diào)錐的存在對(duì)真空發(fā)生器的內(nèi)部流場(chǎng)不會(huì)產(chǎn)生影響；當(dāng)可調(diào)錐進(jìn)入噴管喉部后，對(duì)喉管內(nèi)的流場(chǎng)產(chǎn)生擾動(dòng)，且擾動(dòng)隨可調(diào)錐進(jìn)入噴管喉部距離的增大而變得劇烈，真空發(fā)生器的引射能力逐漸下降，極限真空度逐漸減小。

　　(2)隨著可調(diào)錐進(jìn)入噴管喉部距離的增大，可調(diào)錐上受到的氣壓力合力逐漸增大，該氣壓力有推動(dòng)可調(diào)錐向喉部運(yùn)動(dòng)的作用。

　　(3)通過分析和試驗(yàn)可以獲得可調(diào)錐的調(diào)節(jié)策略為：可調(diào)錐進(jìn)入真空噴管喉部的距離應(yīng)控制在一定的范圍內(nèi)，這一范圍由實(shí)際正常工作所需的最低真空度決定。如果可調(diào)錐進(jìn)入噴管喉部的距離不超過2mm，則可使最低真空度大于65kPa，并能達(dá)到減少約30%耗氣量的效果。