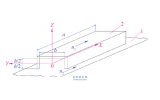
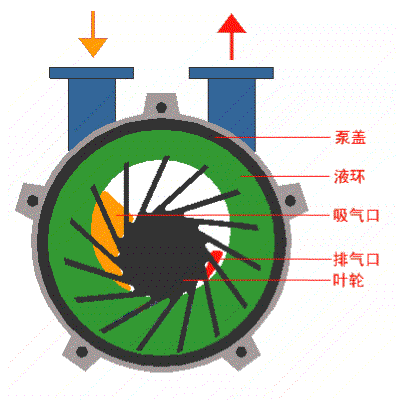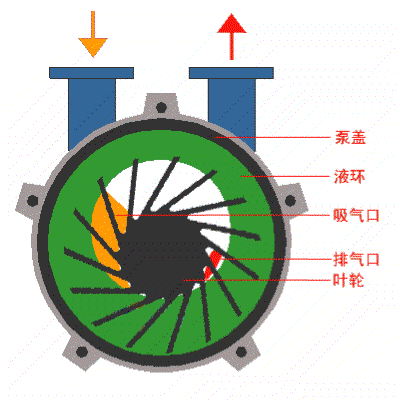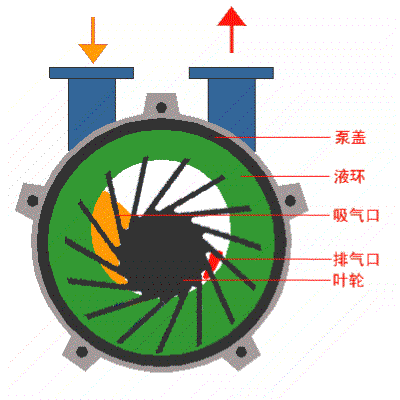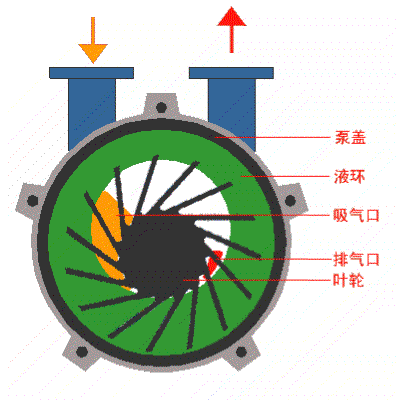
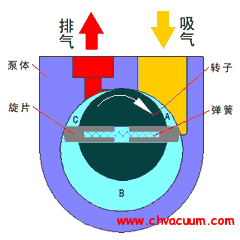
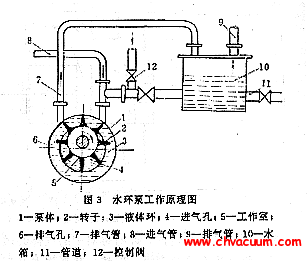
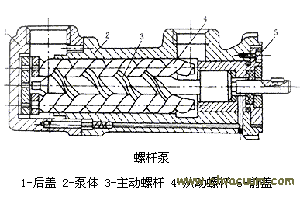
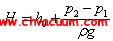渦輪分子泵的抽氣原理
分子泵輸送氣體應滿足二個必要條件:
1、渦輪分子泵必須在分子流狀態下工作。因為當將一定容積的容器中所含氣體的壓力降低時,其中氣體分子的平均自由程則隨之增加。在常壓下空氣分子的平均自由程只有 0.06 μm ,即平均看一個氣體分子只要在空間運動 0.06 μm ,就可能與第二個氣體分子相碰。而在 1.3Pa 時,分子間平均自由程可達 4.4mm 。若平均自由程增加到大于容器壁間的距離時,氣體分子與器壁的碰撞機會將大于氣體分子之間的碰撞機會。在分子流范圍內,氣體分子的平均自由程長度遠大于分子泵葉片之間的間距。當器壁由不動的定子葉片與運動著的轉子葉片組成時,氣體分子就會較多地射向轉子和定子葉片,為形成氣體分子的定向運動打下基礎。
2、分子泵的轉子葉片必須具有與氣體分子速度相近的線速度。具有這樣的高速度才能使氣體分子與動葉片相碰撞后改變隨機散射的特性而作定向運動。
分子泵的轉速越高,對提高分子泵的抽速越有利。實踐表明,對不同分子量的氣體分子其速度越大,泵抽除越困難。例: H2 在空氣中含量甚徽,但由于 H2 分子具有很大的運動速度 ( 最可幾速度為 1557m /s) ,所以分子泵對 H2 的抽吸困難。通過對極限真空中殘余氣體的分析,可發現氫氣比重可達 85 %,而分子量較大,而運動速度慢的油分子所占的比重幾乎為零。這就是分子泵對油蒸氣等高分子量的氣體的壓縮比很高,抽吸效果好的原因。
現以渦輪分子泵的一個葉片為例說明它的抽氣原理。假設一個軸流式單葉列在分子流范圍內以速度 V 運動,如圖 21 所示。
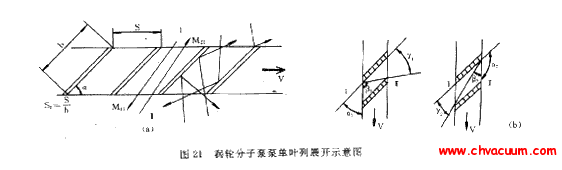
圖21:渦輪分子泵抽氣機理圖
設 I 側為吸入側,Ⅱ側為排氣側。從 I 側向Ⅱ側運動的氣體分子,可分為以下幾種情況:有一部分氣體分子與葉片的端部相碰返回 I 側,一部分氣體分子直接通過葉片槽到達Ⅱ側,還有一部分氣體分子在葉片槽內與葉片壁相碰,其碰撞結果將使一部分到達Ⅱ側,而另一部分氣體分子返回 I 側。同樣,對于Ⅱ側來講,也有一部分氣體分子自Ⅱ側直接抵達 I 側,一部分氣體分子與葉片碰撞后或返回Ⅱ側或抵達 I 側。如圖 21(b) 所示,當 I 側的氣體分子與葉片相碰后反射方向在α1 角內的將又回到 I 側,而反射方向在β1 角內的氣體分子最后將進入到Ⅱ側或散射回 I 側,撞擊在γ1 角內再反射的氣體分子將進入Ⅱ側;同樣,凡是從Ⅱ側入射到葉片上的氣體分子在角α2 內再反射的氣體分子仍回到 I 側,在角γ2 內再反射的氣體分子將散射到 I 側,而在角度β2 內再反射的氣體分子或散射到 I 側或返回Ⅱ側。從α1 、α2 、β1 、β2 、γ1 、γ2 角度的大小關系可以看出:氣體分子從 I 側最終通過葉片進入到Ⅱ側的幾率 M21 大于氣體分子從Ⅱ側最終到達 I 側的幾率 M 21 且葉片的運動速度 V 值越大,效果越明顯,這樣就實現了泵的抽氣目的。葉片的傾角α、葉片弦長 b 、節弦比 S0 、線速度 V 對葉列的抽氣效果都有影響。
設 N1 、 N2 分別表示自 I 側和 I 側入射到葉片的氣體分子流量。而用 W 表示由 I 側到達
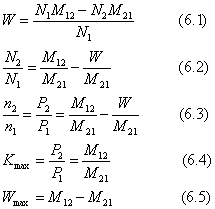
圖:渦輪分子泵抽氣機理計算公式
Ⅱ側的凈氣體分子流量與入射氣體分子流量之比, W 稱何氏系數,則有公式(6 · 1)或公式(6 · 2)
假定葉片兩側溫度相等,而且氣體分子速度分布函數相同,則N2 / N1等是密度比n2 / n1等或是壓縮比P2 / P1。即:(6 · 3)
通過葉列的凈氣體流量為零時,可得最大壓縮比 (6 · 4)
在壓縮比為 1 時 (P2 = P1 ) ,何氏系數最大,即 (6 · 5)
實際的渦輪分子泵都是由多級葉列串聯組成,即按動片、定片、動片、……次序交替排列的。泵的總壓縮比是由葉列的級數決定的。在渦輪分子泵的設計中,應對多級葉列的組合進行優化選配。一般在泵入口側附近應選擇抽速較大的葉片形狀及尺寸,其壓縮比可以相對的小一些。在經過幾級壓縮之后氣體壓力升高,抽速下降了,這時就應該選擇那種壓縮比高、抽速低的葉片形狀。這樣設計可以使整臺泵的抽氣性能得到抽速大、壓縮比高、級數少的理想結果。
計算分子泵葉列傳輸幾率M12和M21的方法很多。例如:積分方程法、角系數法、蒙特卡羅法、矩陣法、工程近似計算法等等。
關于“分子真空泵”其它文章: