基于分形理論，利用MATLAB 開(kāi)發(fā)密封環(huán)端面激光共聚焦掃描圖像分形維數(shù)計(jì)算及分析程序，利用Sierpinski地毯對(duì)程序的計(jì)算結(jié)果進(jìn)行標(biāo)定，計(jì)算不同分割閾值下的圖像分形維數(shù)，給出一種分割閾值的選取方法。研究結(jié)果表明: 設(shè)計(jì)開(kāi)發(fā)的分形維數(shù)計(jì)算程序具有較高的準(zhǔn)確性; 圖像分割閾值的選取對(duì)密封環(huán)端面分形維數(shù)的計(jì)算有重要影響，給出的分割閾值選取方法，能使圖像二值化效果最佳，使掃描圖像能最大程度地反映密封環(huán)端面形貌的分形特征，從而提高密封環(huán)端面形貌定量描述的精確度。

　　密封環(huán)端面的形貌是機(jī)械密封加工和工作過(guò)程中表現(xiàn)出來(lái)的重要特征，它對(duì)機(jī)械密封的摩擦特性和密封特性具有重要影響。研究密封環(huán)摩擦副粗糙表面的固有特性，正確表征摩擦副的表面形貌，對(duì)了解密封端面間的泄漏通道狀況，以及提高機(jī)械密封動(dòng)靜環(huán)接觸端面的磨合質(zhì)量具有重要的意義。

　　20 世紀(jì)70 年代，法國(guó)數(shù)學(xué)家Mandelbrot正式提出并創(chuàng)立了一種探索自然界復(fù)雜形態(tài)的數(shù)學(xué)分支———分形幾何學(xué)。分形幾何能夠在更深層次上深刻地描述、研究和分析普遍存在的雜亂無(wú)章的、不規(guī)則的、隨機(jī)的自然現(xiàn)象，在摩擦磨損領(lǐng)域中引入分形理論實(shí)現(xiàn)了對(duì)摩擦副粗糙表面形貌的科學(xué)的定量描述，從而推動(dòng)了機(jī)械密封端面形貌與探尋密封泄漏通道的研究。在一些基于分形理論的機(jī)械密封端面研究中，大多采用W-M 或M-B 函數(shù)來(lái)表征和模擬密封端面，同時(shí)利用功率譜法和結(jié)構(gòu)函數(shù)法來(lái)研究輪廓曲線的分形特性，但是函數(shù)模擬只能得到統(tǒng)計(jì)意義上的形貌，并不能全部反映密封端面的泄漏通道情況，因此利用掃描圖像來(lái)研究密封端面的形貌特征就具有重要的意義。在以往一些基于掃描圖像的分形特征研究中，多結(jié)合圖像處理技術(shù)對(duì)圖像進(jìn)行預(yù)處理，然后利用計(jì)盒維數(shù)等方式求取二值化后圖像的分形維數(shù)，然而二值化過(guò)程中閾值的選取對(duì)圖像的特征表現(xiàn)和分形維數(shù)計(jì)算具有重要的影響，所選取的分割閾值應(yīng)能最大程度地將密封端面掃描圖像的分形特征表現(xiàn)出來(lái)。

　　本文作者擬利用密封環(huán)端面的激光共聚焦掃描圖像，通過(guò)MATLAB 編程計(jì)算密封端面的分形維數(shù)，討論二值化過(guò)程中分割閾值選取對(duì)分形維數(shù)的影響，給出一種圖像分割閾值的選取方法，突出圖像的自相似特征，從而為密封環(huán)端面的分形表征提供一種快速、精確的新方法。

　　1、基于MATLAB 的分形維數(shù)算法設(shè)計(jì)

　　分形維數(shù)是分形幾何理論中最重要的基本概念之一，目前已經(jīng)有很多維數(shù)的定義，主要包括Hausdorff維數(shù)、計(jì)盒維數(shù)(CBD) 、修正計(jì)盒維數(shù)、填充維數(shù)等。Hausdorff 維數(shù)是分形幾何理論的基礎(chǔ)，可以說(shuō)分形幾何的理論體系是建立在這一基礎(chǔ)之上，但是Hausdorff 維數(shù)只適合分形幾何的理論推導(dǎo)，只能通過(guò)分析的方法獲得一小類(lèi)規(guī)則的純數(shù)學(xué)分形的Hausdorff維數(shù)，它對(duì)實(shí)際應(yīng)用中提出的分形維數(shù)的計(jì)算問(wèn)題無(wú)能為力。鑒于此，人們提出了計(jì)盒維數(shù)的概念，由于計(jì)盒維數(shù)物理含義直觀，易于進(jìn)行程序化計(jì)算，因此得到了廣泛的應(yīng)用。

　　1.1、計(jì)盒維數(shù)的原理

　　設(shè)A 是Rn 空間的任意非空有界子集，對(duì)于任意一個(gè)r>0，Nr(A) 表示用來(lái)覆蓋A 所需邊長(zhǎng)為r 的n維盒子的最小數(shù)目。如果存在一個(gè)數(shù)DB，使得當(dāng)r→0 時(shí)，有

　　計(jì)盒維數(shù)這個(gè)形式的定義在實(shí)際中有廣泛的應(yīng)用。在計(jì)算一個(gè)平面集A 的計(jì)盒維數(shù)時(shí)，可以構(gòu)造一系列邊長(zhǎng)為r 的正方形，然后計(jì)算不同r 值的盒子與A 相交的個(gè)數(shù)Nr(A) ， 這個(gè)維數(shù)是當(dāng)r→0 時(shí)，Nr(A) 增加的對(duì)數(shù)速率，或者可以由函數(shù)lnNr( A) 相對(duì)于lnr 圖的斜率的負(fù)值來(lái)估計(jì)。

　　1.2、程序設(shè)計(jì)

　　圖像在計(jì)算機(jī)中是以矩陣的形式存儲(chǔ)，一幅長(zhǎng)度為M 個(gè)像素，寬度為N 個(gè)像素的圖像，可以看成是一個(gè)M×N 的矩陣，矩陣的每一個(gè)元素代表一個(gè)像素，元素的值是像素點(diǎn)顏色或索引色。利用激光共聚焦獲得的密封環(huán)端面圖像是RGB 格式，無(wú)法直接進(jìn)行計(jì)盒維數(shù)的計(jì)算，因此需要對(duì)圖像進(jìn)行預(yù)處理，包括灰度變換、平滑濾波、降噪等，再選取一個(gè)合適的分割閾值，將圖像二值化，這樣就將圖像處理成只包含0 (孔隙) 和1(固體骨架) 的二值矩陣。根據(jù)計(jì)盒維數(shù)的原理，可以通過(guò)MATLAB 編寫(xiě)程序計(jì)算計(jì)盒維數(shù)，步驟如下：

　　(1) 讀取二值化的密封環(huán)端面圖像，并將其數(shù)值矩陣賦值給變量H；

　　(2) 用不同邊長(zhǎng)尺寸的正方形盒子對(duì)矩陣H 進(jìn)行覆蓋，統(tǒng)計(jì)在不同尺寸r 下包含目標(biāo)像素(0—孔隙) 的盒子數(shù)，計(jì)入數(shù)組Nr中；

　　(3) 在雙對(duì)數(shù)坐標(biāo)中利用最小二乘法對(duì)(lnr，lnNr) 進(jìn)行擬合，得到直線斜率的負(fù)數(shù)即為圖像的計(jì)盒維數(shù)。

　　程序的流程圖如圖1 所示。

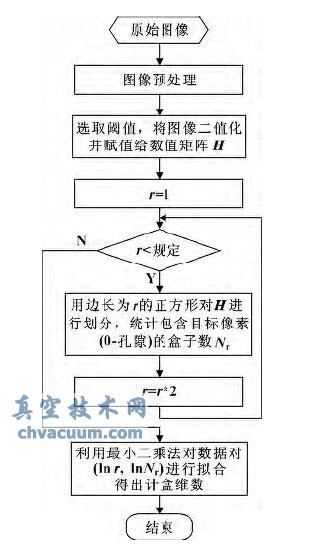
圖1 MATLAB 計(jì)算計(jì)盒維數(shù)程序流程圖

　　1.3、程序驗(yàn)證

　　為了驗(yàn)證設(shè)計(jì)程序的正確性，采用5級(jí)Sierpinski地毯作為標(biāo)定圖像，將計(jì)算結(jié)果與標(biāo)準(zhǔn)結(jié)果進(jìn)行對(duì)比。可以看出，本文的計(jì)算結(jié)果與理論維數(shù)相對(duì)誤差非常小，說(shuō)明本文作者設(shè)計(jì)的程序是可行的，同時(shí)也具有很高的精確度。

2、結(jié)論

　　(1) 利用MATLAB 圖像處理，結(jié)合分形的基本理論，設(shè)計(jì)開(kāi)發(fā)了基于MATLAB的分形維數(shù)計(jì)算分析程序，利用Sierpinski地毯進(jìn)行標(biāo)定，驗(yàn)了程序的可行性和準(zhǔn)確性。

　　(2) 分割閾值的選取對(duì)分形維數(shù)的計(jì)算具有重要影響，隨著閾值的增大，分形維數(shù)總體上呈逐漸增大的趨勢(shì)；給出的分割閾值選取的方法，能夠使密封環(huán)端面圖像中的孔隙結(jié)構(gòu)最大化地表現(xiàn)出來(lái)，提高了分形維數(shù)計(jì)算的精確度。

　　(3) 密封端面形貌具有高度的自相似特征，利用密封端面共聚焦掃描圖像結(jié)合分形理論，可以實(shí)現(xiàn)對(duì)密封端面形貌的快速、準(zhǔn)確的定量描述，這對(duì)于揭示密封端面的泄漏通道具有重要的意義。