由于真空玻璃的導熱系數測量復雜，本文提出一種基于非穩態傳熱過程的軟測量表征真空玻璃導熱系數的模型。首先，在連續介質與半無限大物體的前提下，采用能量守恒定律與拉普拉斯變換法，對數學物理模型進行求解，建立非加熱面的中心溫度計算公式。然后，利用數值仿真軟件FLUENT 對物理模型進行溫度場仿真。

　　仿真結果表明：檢測時間少于5 分鐘，達到節約時間的目的；為保證溫度測量準確，取多個測量點的測量值；為減小測量誤差，采用圓形加熱片時，加熱片的半徑與真空玻璃厚度之比要大于3。這些為后續研究真空玻璃導熱系數與溫度變化之間的關系奠定一定的理論和應用基礎，對實驗有指導意義，為真空玻璃導熱系數的在線檢測和其過程的優化控制提供指導。

　　在推進節能型社會建設的進程中，建筑節能是不能忽視的重要方面。門窗耗費的能量不容小覷。具有自主知識產權的真空玻璃是一種性能優異的新型節能建材，在全社會節能減排的趨勢下，受到了人們的廣泛關注。使用真空玻璃門窗后，不僅明顯節省了空調的制熱制冷費用，極大地提高了居室環境的舒適度，而且由于真空玻璃結構上的特點，即真空層的存在，阻隔了聲音的傳遞，可保持室內寧靜空間，減小噪聲污染。同時，真空玻璃的熱阻很大，真空腔內無空氣，也無水汽分子，即使室內外溫差達到50℃也不會出現結露現象，令人視野清晰開闊。

　　由于真空玻璃暴露在房屋外面，在使用過程中很容易受到外界環境的腐蝕及不可預料的外力沖擊作用，這些都會使真空玻璃的性能退化甚至結構破損，從而失去其節能功能。周期性地對真空玻璃性能進行檢測與監測，可以保證真空玻璃的健康狀態及其使用壽命，是保證節能建筑發揮節能功效所必須的工作內容。

　　國內外廣泛使用的熱傳導性能測試方法尚無統一的標準，主要使用穩態測量方法。穩態熱傳導測試方法的基本原理如下：首先被測試的樣品兩個表面形成恒定的溫差，平衡一段時間后，試樣內部的溫度分布不再隨時間變化，即進入穩態熱量傳遞狀態，試樣內部每一位置通過的熱流量相等，最后利用熱流量、溫差和導熱系數之間的關系反解出導熱系數。不過，由于真空玻璃熱擴散系數很小，為使試樣達到穩態熱量傳遞狀態，需要較長的實驗時間。同時，為了使熱流單向一維流動，試驗裝置必須配備良好的絕熱層，同時，樣品邊界附近的漏熱現象將影響到測試結果，而且為了保持被測試的樣品兩個表面的溫差恒定，試驗裝置需具有良好的恒溫系統，從而使得試驗裝置較復雜和冗雜。

　　文獻1 提出在相同熱源下，真空玻璃非熱源側溫度與傳熱性能相關，本文在此基礎上，提出非穩態傳熱模型，建立非熱源側溫度計算方法并利用CFD 數值仿真技術，進行溫度數據分析，并提出在實驗中測量溫度要注意的事項。

1、真空玻璃

1.1、物理模型

　　真空玻璃通常是由兩片玻璃組成，在中間放置微小的支撐物以均勻隔開，在周邊采用玻璃焊料熔融封接。然后，通過抽真空后封裝抽氣孔或者在真空環境下熔封玻璃周邊等方法使玻璃之間形成真空層，如圖1 所示。

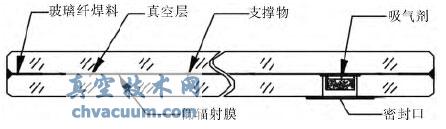
圖1 真空玻璃基本結構

1.2、數學模型

　　將真空玻璃在宏觀上用均質平板玻璃來代替不連續的支柱排列，應用連續介質假設，將真空玻璃用某一均勻連續介質作為其等價介質，其溫度、密度等物理參數都是空間的連續函數，表征其等效的物理性質。

　　當物體的溫度隨著時間的變化而隨之變化時，這個導熱過程稱之為非穩態導熱。導熱微分方程及初始條件與邊界條件一起，才能完整地描述一個特定的非穩態導熱問題。結合傅立葉導熱定律與半無窮假設，如圖2 所示：將在加熱過程中的真空玻璃看作是無限大的，即在時間τ=0 時，位置x=0 處的表面受到擾動，溫度t 沿僅且僅沿x 軸方向一維傳遞。

圖2 半無限大物體示意

2、CFD仿真

　　數值仿真技術可以幫助人們完成從最初的基本結構設計到最后的參數優化，利用CFD 軟件可以使人們細致入微地觀察全部情況。通過數學方程描述物理問題的數值求解的基本思想可概括如下：在時間坐標系與空間坐標系中，原本是連續變化的物理量的場，通過網格劃分手段，用數量極多(可以代表物理量的場的特性)但有限個(數學方程可以解出)離散點上的值的來代替原來的物理量的場，這樣求解關于這些離散點上的值的代數方程，就可以獲得離散點上被求的物理量的值，上述基本步驟可以如圖3 來表示：

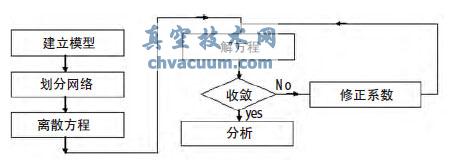
圖3 流程框架

　　本文研究內容基于UG、ICEM 和FLUENT 商用軟件。運行的計算機主要配置為：處理器：Intel(R)Pentium (R)CPU B950-2.10GHz；內存4GB；操作系統：Windows7 旗艦版。幾何模型的準確性和網格劃分的質量與數值仿真結果的可靠性息息相關。所以在UG 軟件中建立真空玻璃的幾何模型時，應盡量與實際情況相一致；用ICEM 軟件劃分網格后，要注意檢查網格質量。在本文中，所有模型都是基于UG8.0版本做出，并導出ANSYS ICEM 可以識別的IGES文件，在ANSYS ICEM 中可以做出質量較高的網格，如圖4-1 所示。

　　考慮到在實驗過程中，溫度是唯一的測量量，真空技術網（http://smsksx.com/）認為它的準確性十分重要。在數學模型中，假設了溫度只沿x 軸方向進行一維導熱，這樣，理論上，只要測得溫度與時間的變化關系即可得出導熱系數λ 表征的值。不過，在實驗中，不得不考慮到溫度的y 軸傳熱過程，即徑向傳熱過程。所以，在實驗中就必須合理地解決測溫點的選取問題，提高實驗的準確性及復現性。

2.1、測溫點的選取

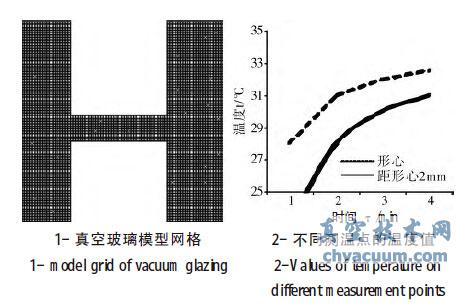
圖4 網格劃分及溫度變化

　　由圖4 可以看出，在5 分鐘內完全可以測量多個測量點，完成實驗。由于支柱和徑向熱量傳輸的影響，右側形心處的溫度較其他點溫度較高，同時為了避免在實驗中出現的隨機將測溫點布置在溫度較高附近，所以，測溫點不能僅僅選擇一個，而是要在形心某一半徑范圍內布置多個，取各個溫度值，求和作均值化。

2.2、加熱片的半徑

　　為了構造半無限大條件，降低徑向傳熱的影響，加熱片的面積越大越好。如圖5 所示，模型厚度10mm，在不同面積加熱片時，測溫點的溫度變化情況。隨著加熱片面積的增大，也越來越符合半無限大物體的特性，徑向導熱對測量點的溫度影響逐漸變小，相同時刻的溫度誤差越來越小。當加熱片面積增大到一定程度，對精度的貢獻及在工程應用上的影響，可以忽略不計。

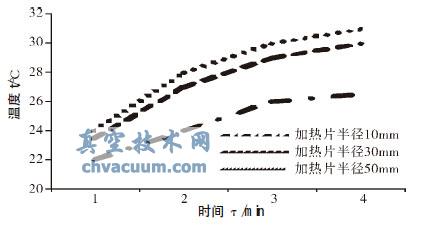
圖5 測溫點溫度與加熱片面積關系

3、結論

　　在全球低碳節能浪潮下，真空玻璃將隨著產業化進程的加快獲得越來越廣泛的應用。其相關性能參數的測量也愈發重要。由此，本文建立了非穩態傳熱模型，得出非加熱面的中心溫度計算公式，并通過CFD 仿真，分析模型的可行性及指導下一步實驗相關測量注意事項。

　　3.1、與穩態測試方法相比，非穩態方法是測量試樣升溫趨勢的動態過程，測試時間長短可以靈活掌控，滿足短時間的測試要求。

　　3.2、該方法測量出表征導熱系數的同時，也可實現對表征熱擴散系數的分析確定。對于評價自身熱工性能、分析非穩態過程的研究和應用具有重要意義。

　　3.3、通過建立合理化的傳熱模型，得到對真空玻璃傳熱后側(非熱源側)中心溫度實時測量，可以獲知真空玻璃的隔熱性能優劣和真空玻璃質量的結論。

　　3.4、溫度測量是下一步實踐中的重點，在測溫點及加熱片的選取問題中，通過仿真，得出了取多個測量點的測量值，然后求和取均值作為真值；加熱片的半徑與真空玻璃厚度之比要大于3，具有指導意義。