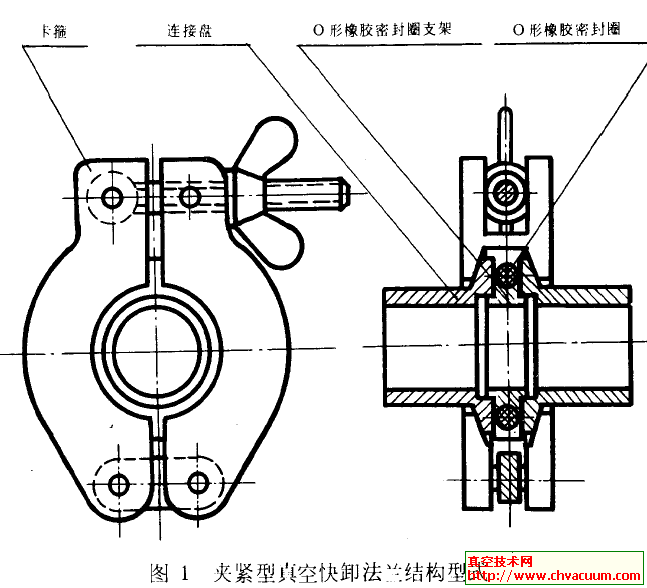
機械密封端面黏著磨損分形模型的建立
機械密封端面微凸體的接觸特性
對于端面材料采用軟─硬組對形式的機械密封,將硬質環與軟質環的接觸簡化為剛性理想光滑平面與粗糙表面的接觸后,密封端面沿周向展開后的接觸模型如圖2 所示。
根據W - M 分形函數,粗糙表面上面積為a 的接觸微凸體在-l /2 ~l /2 范圍內的輪廓線可近似為余弦波( 參見圖2) 。變形前的微凸體可定義為:
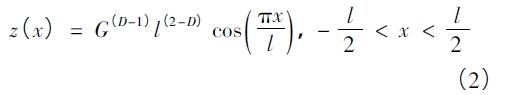
式中z( x) ———微凸體輪廓高度,m;x ———輪廓的位置坐標,m;G ———輪廓特征尺度系數,m;D———輪廓分形維,1< D < 2
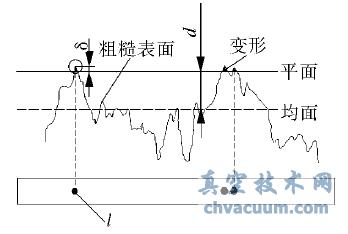
(a) 粗糙面與光滑面的接觸
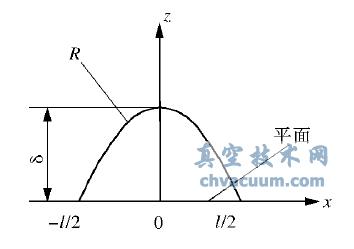
(b) 微凸面變形前幾何形狀
圖2 機械密封端面接觸模型
微凸體的接觸面積a 在輪廓線上對應于接觸長度l。兩者之間的關系為:
l = 2( a / π) 1 /2 (3)
機械密封端面微凸體的變形方式包括彈性、彈塑性和塑性3 種。依據分形理論經分析可得,微凸體臨界彈性變形微接觸面積ac為:
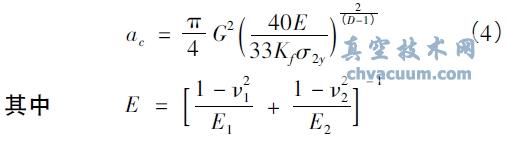
式中E———綜合彈性模量,Pa;E1,E2———硬質環、軟質環材料的彈性模量,Pa;ν1,ν2———硬質環、軟質環材料的泊松比;Kf———摩擦校正系數,Kf = 1 -0.228 fc;fc———微凸體接觸摩擦因數,即干摩擦因數;σ2y———軟質環材料的抗壓屈服強度,Pa
當微凸體接觸面積a > ac時,該接觸微凸體處于彈性變形; 當a≤ac時,處于塑性或彈塑性變形。
由分形理論可得,密封端面微凸體接觸面積分布函數為:
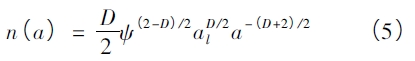
式中ψ———分形區域擴展系數;al———最大微凸體接觸面積,m2
分形區域擴展系數ψ 和最大微凸體接觸面積al計算式:
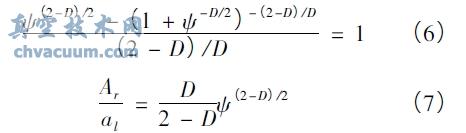
式中Ar———密封端面真實接觸面積,m2
機械密封端面接觸微凸體體積
由于密封端面形貌具有各向同性的特征,因此,可將密封端面微凸體近似為軸對稱體,如圖3所示,其軸截面輪廓曲線滿足式(2) 所示的關系式,其底邊圓半徑為1 /2,則單個微凸體的體積V(a) 為:
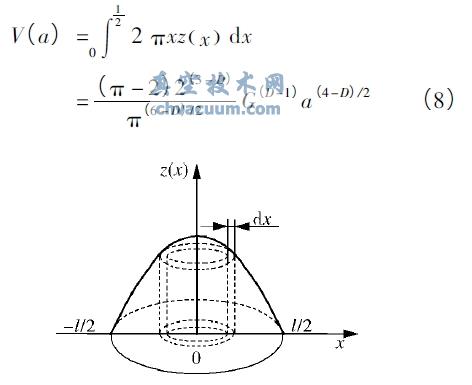
圖3 微凸體體積
機械密封端面黏著磨損分形模型
由真空技術網上一文(機械密封端面磨損率的一種簡易計算方法http://smsksx.com/mechanical-seal/053241.html)中的Archard 磨損理論可知,在接觸載荷的作用下,機械密封軟質環端面部分接觸微凸體產生塑性或彈塑性變形,從而形成黏著結點。同時,在摩擦力的作用下黏著結點被剪斷,形成磨屑,從而導致軟質環端面產生磨損。
當密封端面相對滑動距離為l 時,在黏著結點處將產生一個微凸體的磨屑。由式(4 ) 、式(5) 、式(7) 和式(8) 可得,在整個接觸端面上所有黏著結點產生的磨屑總體積ΔV 為:

式中Aa———密封端面名義接觸面積,m2;A*r ———密封端面量綱1 真實接觸面積,

式中apt———微凸體臨界塑性變形微接觸面積,m2根據機械密封端面間最大微凸體接觸面積al與臨界彈性變形微接觸面積ac及臨界塑性變形微接觸面積apt相比較的大小關系,機械密封端面量綱1 真實接觸面積A*r與密封端面比壓pc的關系可分為3 種情況,其具體表達式參見文獻。
對所有黏著結點,產生ΔV 體積的磨屑時,摩擦副端面的相對滑動時間t 為:

考慮并非所有黏著結點都會形成磨屑,引入分形磨損系數KF(KF《1) 表示形成磨屑的黏著結點占全部黏著結點的百分比,即黏著結點產生磨屑的概率,則根據Archard 磨損理論,可得機械密封軟質環端面在整個名義接觸面上的磨損率γ為:

式(12) 即為機械密封軟質環端面磨損率的分形表達式。當分形磨損系數KF已知,由式(12) 并結合文獻中求解量綱1 真實接觸面積A*r
的相關公式,即可求出一定工作參數和端面分形參數時的軟質環端面磨損率。由于在整個磨損過程中機械密封軟質環端面的形貌是動態變化的,即分形參數D 和G 是時變的,故磨損率也是時變的,式(12) 為一動態方程,這正是對材料磨損特性時變性的定量描述。