針對傳統基于連續流假設的N-S方程無法準確描述約束環內稀薄氣體問題，采取二次優化策略，確定了CFD-ACE +中基于努森數的粘度修正公式參數a、b 的最優值分別為0.12 和1.40。對約束環內氣體流動進行模擬仿真，結果表明：利用本文中的粘度修正公式，可以使約束環內稀薄氣體的模擬仿真結果與實驗測量值相一致，該公式在較寬的入口流量范圍(200 ～ 2000mL/min 之間) 內應用均可控制仿真結果的相對偏差在±3%之內，其精度滿足實際工程需要；并且，獲得粘度修正公式參數的方法同樣適用其它微通道內稀薄氣體的研究，對相同工況下類似刻蝕腔室內氣流仿真、新機型設計等亦有很大的指導意義。

　　在等離子體刻蝕設備中，約束環是位于等離子體工藝處理區和排氣區域之間的重要部件，其作用是控制反應氣體及其副產物的排出、中和其中的帶電粒子，從而將等離子體放電基本約束在處理區域。等離子體刻蝕要求在低壓下進行，腔室內的氣壓不能超過一定的閾值( 通常低于13.3 Pa) ，對于新型抽氣系統的設計，由于等離子體刻蝕實驗費用昂貴，工程師需要通過模擬仿真確定腔室內氣壓是否滿足低壓要求，所以數值模擬工具(如CFD-ACE +) 在新型刻蝕設備的研發中應用潛力巨大。約束環由相互等間隔( 一般小于2 mm) 的多個環組成，環與環之間形成大長寬比( 大于10) 的微通道。由于約束環的特征長度與平均分子自由程相當甚至更小，努森數Kn(表征氣體稀薄程度的物理量) 一般大于0.1，所以約束環內的氣體流動已屬于非連續流區，傳統的基于連續流的納維-斯托克斯方程(N-S) 方程不再成立。由于約束環結構的特殊性，目前的數值模擬方法不能正確模擬約束環內稀薄氣體的流動，使得仿真結果無法準確的預測腔室氣壓。

　　目前，基于實驗宏觀理論修正法成為分析仿真微通道內流體的一種解決方案。該方法通過對宏觀流體理論的傳熱學理論、基本方程、邊界條件和物性參數等作適度修正，可以將宏觀流體理論應用于微流體計算與仿真，并達到較理想的仿真結果。Pfahler 等認為：微流體計算時，可在N-S方程中引入當量粘度μeff代替μ0，使計算結果與試驗觀察值一致。并且，對于流量、管長一定的微通道，只能修正流體的粘度。Polard 和Present等提出了一個基于努森數Kn 的粘度修正公式，但是該公式依賴一個可變的參數；Beskoket 等在此基礎上發現該可變參數也依賴于努森數Kn，結合粘度修正模型和滑移速度模型，Karniadakis 等發現他們的結果可以與直接模擬蒙特卡洛(DSMC) 結果以及線性玻爾茲曼方法的結果達到很好得吻合，但是由于該公式的參數依賴于努森數Kn，限制了其應用。

　　本文從連續介質N-S方程出發，面對約束環微通道內的稀薄氣體流動特性，結合已有的一階滑移邊界模型和粘度修正模型擴展N-S方程，使其能夠求解約束環內過渡流區的流動特性。本文的重點在于采用數值模擬手段確定粘度修正公式的參數，使得仿真結果與實驗測量數據相一致。將仿真數據逼近實驗數據的過程看成優化問題，在彭磊等提出的基于動態徑向基函數代理模型的優化策略基礎上進行一定的簡化和改進，基于樣本點構造法先后進行兩次優化，初次優化確定縮小的優化區間，在縮小的優化區間內加密樣本點進行第二次優化，這樣可以通過較少的仿真模擬次數獲得高精度的仿真結果。在類似結構的刻蝕腔室的設計中，可以采用本文方法，得到更加真實可靠的數值模擬結果，極大縮短設計周期。

　　1、物理模型

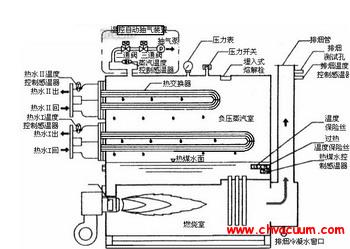
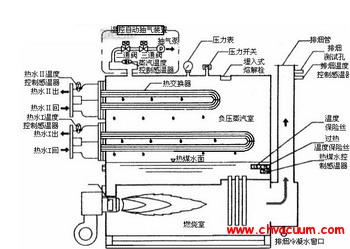
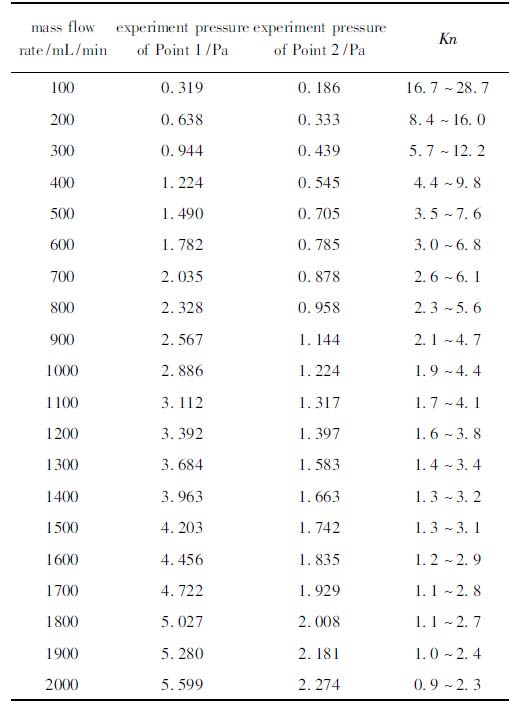
　　在等離子體刻蝕過程中，針對不同的刻蝕對象選取不同的反應氣體，反應氣體經噴淋板進入刻蝕腔室內，在工藝處理區內發生復雜的物理化學反應。如圖1 所示，反應后氣體經約束環到達排氣區域后被氣泵抽走。由于本文只關注刻蝕腔室流場的分布，且在工業界，出于環保和測試成本的考慮，常常選取惰性氣體(如氬氣、氮氣等) 作為實驗測試氣體，故在本文中為了簡化問題，反應氣體成分選取業界最常用的實驗測試氣體———氬氣。在工藝處理區和排氣區域選取了P1、P2兩個測量點(見圖1) ，分別測量這兩點處的壓強。實驗測量結果見表1。

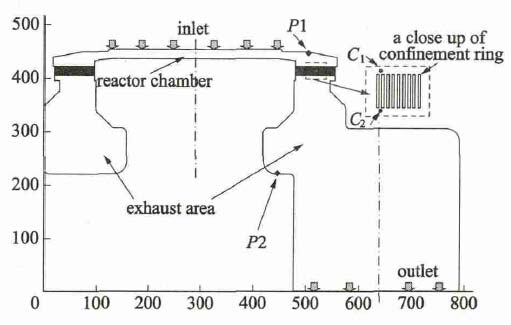
圖1 刻蝕腔室結構示意圖

表1 P1、P2 兩點實驗測量值

　　5、結論

　　在等離子體刻蝕設備研發中，刻蝕腔室內流場分布是設計人員最為關心的問題之一，而約束環是影響流場分布的重要部件。本文針對約束環微通道內稀薄氣體流動進行了研究，在連續流假設基礎上，采用CFD-ACE +中提供的氣體粘度修正公式，提出了一種確定粘度修正參數的方法。采用該方法確定的粘度修正公式，可以使得數值模擬結果和實驗觀測值相一致。這樣，在對等離子體刻蝕腔室內流場進行模擬仿真時，結果更加真實可靠，進而有助于促進新機型的設計和研發。

　　本文主要結論如下：

　　①利用實驗測量值，確定了基于努森數Kn 的粘度修正公式參數，參數a、b 的最佳值分別為0.12 和1.40；

　　②該粘度修正公式對較寬的入口流量范圍(200～2000 mL/min) 均可適用，相比于實驗測量值，其仿真相對誤差可以控制在±3%內；

　　③通過二次優化策略，只需較少地模擬試驗次數即可確定粘度修正公式的參數，該方法可推廣應用到其它微通道內稀薄氣體問題研究中；

　　④事實上，該二次優化策略并不局限于兩次優化，如果兩次優化不能滿足精度要求，則可繼續進行更多次優化計算，直至達到足夠的精度。