真空管道高速列車氣動噪聲源特性分析
為研究真空管道中高速列車的氣動噪聲源特性,建立低壓環境下真空管道高速列車空氣動力學計算的流體模型、數學模型和數值模型,以及高速列車偶極子噪聲源和四極子噪聲源的計算模型,研究管道壓力、列車速度和阻塞比對真空管道高速列車偶極子噪聲源和四極子噪聲源的影響。計算結果表明,在低壓(103~104Pa)環境下,真空管道中的空氣流動可以采用連續介質模型描述。高速列車偶極子噪聲源和四極子噪聲源均與車速的對數成線性關系,當車速為600km/h時,四極子噪聲源較小,偶極子噪聲源占據主導地位,隨著列車速度的提高,四極子噪聲源變得明顯,并占據主導地位。降低管道壓力和阻塞比可以有效減小高速列車氣動噪聲源的強度。
隨著列車運行速度的提高及高速列車運營的日益普遍,許多在低速時被合理忽略的問題都逐漸浮出水面,并且在很大程度上影響著列車的提速。與普通列車相比,高速列車所處的動態環境發生了質的變化,由機械、電氣作用為主,變成了以氣動作用為主。高速列車的氣動阻力與運動速度的二次方成正比,且高速列車運行產生的氣動噪聲更與運行速度的六次方到八次方成正比。這是任何地面形式的地面交通工具都無法避免的客觀規律。在地表稠密大氣層中運行的高速交通工具,其最高速度都不宜超過400km/h。為在地面上獲得更高的運行速度,其根本途徑只能是改變介質的密度。干線飛機的巡航高度達到萬米,也是為了擺脫地表稠密大氣層的作用。地面列車無法飛到萬米高空,但是可以利用密閉的管道,通過降低管道內部的壓力,相當于在列車周圍創造出低密度的介質環境,可以擺脫氣動阻力和氣動噪聲的困擾,在理論上可以實現任意高速度的運行,真空管道高速交通作為下一代高速運載工具的想法應運而生。從全球范圍來看,真空管道高速交通目前尚無先例可供參考,對真空管道高速交通的設想主要有兩種:美國的ETT系統和瑞士的超高速地鐵。美國ETT公司只是對真空管道運輸系統的總體設想進行了介紹,并未有對其列車空氣動力學問題進行深入研究。瑞士超高速地鐵工程研究的主要課題中雖然包含了高速車輛與管道內的空氣動力學問題,但是只局限于大氣壓力為104Pa,列車運行速度為400~500km/h條件下的列車空氣動力學特性。在國內,2004年12月18日,由沈志云、鐘山聯合發起的/真空管道高速交通0院士學術報告會在西南交通大學順利召開,對真空管道高速交通系統的科學性、現實性、發展前景及重大意義等進行討論。真空管道高速列車空氣動力學的研究正處于起步階段,相關的研究工作還非常少,文獻采用二維不可壓縮模型研究了真空管道中阻塞比對列車氣動阻力的影響特性。文獻采用二維可壓縮模型研究了真空管道高速列車氣動阻力與列車速度、阻塞比和管道壓力的關系。文獻采用三維可壓縮模型研究了真空管道高速列車氣動阻力與列車速度、阻塞比和管道壓力的關系。目前已有的研究工作主要是關注真空管道中高速列車的氣動阻力特性,而沒有文獻涉及真空管道中高速列車的氣動噪聲問題,在真空管道中,高速列車的外部氣動噪聲不會對環境產生影響,但高速列車的車內氣動噪聲會影響旅客的乘坐舒適性。真空管道中高速列車的車內氣動噪聲與車身表面的氣動噪聲源有關,本文采用三維可壓縮模型對真空管道高速列車的氣動噪聲源進行數值計算,并研究列車速度、阻塞比和管道壓力對列車氣動噪聲源的影響。
1、真空管道高速列車空氣動力學模型
1.1、流體模型
隨著真空管道內部管道壓力的減小,真空管道中氣體的密度隨著減小,氣體的稀薄效應變得越來越明顯。氣體流動的稀薄程度可以采用Knudsen數表示。Knudsen數(Kn)定義為分子平均自由程K與流動特征長度L的比值,即
![]()
錢學森最早根據稀薄程度將氣體流動分為三大領域,即滑移領域(0.01<Kn<0.1)、過渡領域(0.1<Kn<10)和自由分子流領域(Kn>10)。而當Kn<0.01時,可以認為流動處于連續領域內,在這一領域內可以采用連續介質模型描述氣體的流動。對于氣體而言,分子平均自由程是分子兩次碰撞之間通過的平均距離。當采用硬球模型時,分子平均自由程可以表示為

式中,n表示分子的數密度,d表示分子直徑。壓力和溫度滿足完全氣體關系式
![]()
式中,p表示壓力;T表示溫度;n表示氣體的數量密度;kB表示Boltzmann常數,kB=1.3805×10-23。從而,分子的平均自由程可以表示為
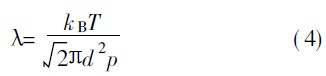
當溫度為298K時,標準大氣壓下的分子的平均自由程為K=6.11 ×10-8 m。本文中,真空管道內的管道壓力變化范圍是:103~104Pa,相應的分子平均自由程的變化范圍是6.11×10-7~6.11×10-6 m。高速列車繞流流動的特征長度可取為列車的高度(對于典型的高速列車,其高度值可以取為3.7m)。由此可知,本文中,真空管道中高速列車周圍流場流動的Knudsen數最大值為
![]()
由此可知,真空管道中高速列車的流場可以采用連續介質模型描述。
4、結論
本文建立真空管道中高速列車空氣動力學模型和氣動噪聲源分析模型,較為系統地研究了管道壓力、列車速度和阻塞比對高速列車表面偶極子噪聲源和四極子噪聲源的影響,主要有如下結論:
(1)在低壓(103~104Pa)環境下,真空管道中的氣體流動可以采用連續介質模型描述。
(2)真空管道中,高速列車偶極子噪聲源和四極子噪聲源與列車速度的對數成線性關系。當列車速度較低時,四極子噪聲源較小,偶極子噪聲源占據主導地位,隨著列車運行速度的提高,四極子噪聲源變得越來越明顯,并超過偶極子噪聲源而占據主導地位。
(3)真空管道中,高速列車偶極子噪聲源和四極子噪聲源隨著管道壓力和阻塞比的增加而增大,減小管道壓力和阻塞比可以有效降低高速列車的氣動噪聲源。
(4)對于實際的真空管道高速交通系統,在進行管道壓力和阻塞比的最優設計時,既需要考慮氣動特性的影響,還需要考慮經濟成本的影響。






