分析了承壓閥門內(nèi)漏過程中流體流動狀態(tài),以及聲源產(chǎn)生機理,建立了閥門泄漏產(chǎn)生的聲源信號幅度與內(nèi)漏率的一般關(guān)系. 利用研制的實驗臺對閥門內(nèi)漏進行檢測實驗,并探討了泄漏時閥門開度、兩側(cè)壓差等狀態(tài)變化時的聲學(xué)特性. 研究結(jié)果表明,閥門湍流流場產(chǎn)生的聲源主要為四極子聲源,其聲能隨著壓差和流速的增大而增強. 因此,可以利用聲學(xué)方法檢測承壓閥門是否存在泄漏和估計泄漏率。

0、引言

　　閥門作為一種通用的機械產(chǎn)品,其安全性一直是人們關(guān)注的焦點. 石油、石化是閥門使用率非常高的行業(yè),據(jù)統(tǒng)計,購買閥門的費用相當(dāng)于一個新建工廠投資的8 %. 在用承壓閥門中有相當(dāng)數(shù)量的閥門因磨損、腐蝕或其他多種原因往往會出現(xiàn)內(nèi)外滲漏或泄漏,一般情況內(nèi)漏很難發(fā)現(xiàn),內(nèi)漏若不及時發(fā)現(xiàn)和處理會導(dǎo)致嚴(yán)重的事故(如輸送流體大量流失、串線、起火甚至爆炸,污染環(huán)境等) ,因此迫切需要一種實用高效的閥門內(nèi)漏檢測技術(shù). 聲學(xué)檢測具有在線、動態(tài)及快速、經(jīng)濟的特點,既可保證閥門的安全使用,又可為維修決策提供依據(jù),降低更換費用 . 因此,聲學(xué)方法是檢測承壓閥門內(nèi)漏的有效方法.

　　國外從20 世紀(jì)60 年代起就開展了閥門泄漏檢測技術(shù)的研究,目前部分研究成果已經(jīng)得到了廣泛應(yīng)用. 筆者通過對閥門內(nèi)漏過程的理論分析和實驗研究,確定了閥門內(nèi)漏率與聲學(xué)參量的一般關(guān)系式,進而可判斷閥門是否有內(nèi)漏,并確定內(nèi)漏量.

1、閥門內(nèi)漏產(chǎn)生聲源的數(shù)學(xué)模型

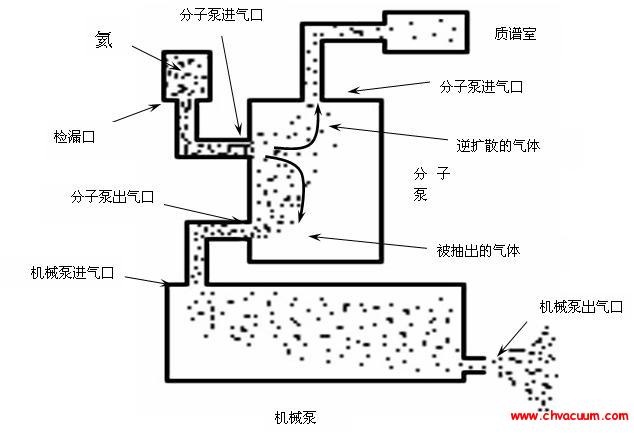
　　假設(shè)內(nèi)漏模型為充分的泄漏噴射,并分成3 個區(qū)域:混合區(qū)、過渡區(qū)和充分發(fā)展區(qū),見圖1. 據(jù)真空技術(shù)網(wǎng)另文介紹:混合區(qū)的延伸距離大約是閥門直徑D 的4.0～4.5 倍,過渡區(qū)距離大致擴展到D 的10 倍. 沿泄漏表面,漏口附近聲壓較低,在3 至4 倍直徑的距離內(nèi)迅速增加到極大值,以后又慢慢降低,泄漏聲音大部分來自混合區(qū)和過渡區(qū)的湍流運動, 高頻噪聲主要產(chǎn)生在噴口附近,低頻噪聲產(chǎn)生在下游,頻譜峰在混合區(qū)的尖端附近.

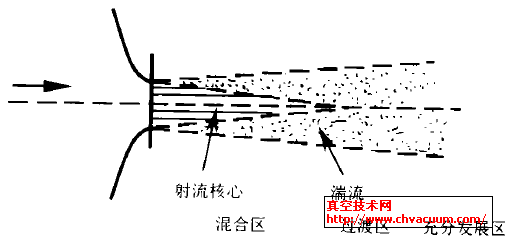
圖1 　閥門內(nèi)漏分析模型

　　在噴口稍遠的地方為過渡區(qū). 在過渡區(qū)中處處充滿湍流,平均速度隨噴射距離的增加而漸減,射流寬度逐漸擴展. 在噴口更遠的地方, 流體成為完全湍流運動, 這就是充分?jǐn)U展區(qū). 在這個區(qū)域里流速逐漸降低以至完全消失,湍流強度變小,產(chǎn)生的聲信號為低頻性.

　　閥門內(nèi)漏時聲源產(chǎn)生的基礎(chǔ)是流體內(nèi)湍流產(chǎn)生的波動壓力場,流體內(nèi)漏所激發(fā)的應(yīng)力波為連續(xù)信號且具有較寬的頻率范圍. 湍流是流體流動不穩(wěn)定的一種情況,在其內(nèi)部慣性的影響遠大于黏性阻力的影響而處于支配地位. 臨界流速vc 是該流動條件下層流與紊流的轉(zhuǎn)變流速,它與流體的黏度μ成正比,與流體的密度ρ和管徑d 成反比,即雷諾數(shù)Rec 由下式表示:

　　已經(jīng)發(fā)現(xiàn)當(dāng)雷諾數(shù)在10³ 到10⁴ 之間時湍流開始發(fā)生,臨界雷諾數(shù)穩(wěn)定在2.0 ×10³ 左右,其中公認(rèn)希勒(Schil Ier) 的實驗值Rec = 2.3 ×10³ ,這種情況可用于估計是否一個給定的泄漏能發(fā)生有效的聲源.設(shè)質(zhì)量密度為ρ( x , t) ,速度場為v ( x , t) . 假設(shè)場中無質(zhì)量生成(因此, Q = 0) ,質(zhì)量守恒方程為

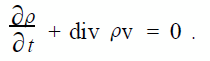
　　微分形式的守恒方程為

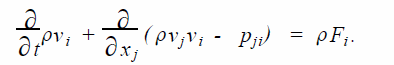
　　利用式(2) , (3) 消去含ρvi 項,可推導(dǎo)出如下的非齊次波動方程

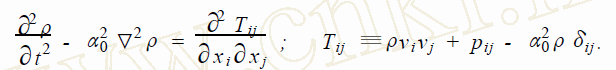
　　解方程(4) 得

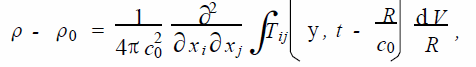
　　忽略黏滯應(yīng)力和熱應(yīng)力的影響,則聲功率p 為

　　在沒有固體的自由噴流中,馬赫數(shù)小,聲源也小時,聲發(fā)射的總功率與特征速度的8 次方成正比(所謂四極子聲源的特性) . 可是在固體邊界效應(yīng)大的情況下,聲源的尺寸比波長小時,發(fā)射聲的總功率與特征速度的6 次方成正比. 考慮到一般情況,發(fā)射聲的總功率可表示成與速度的n 次方( n > 1) 成比例. 即在一定的范圍內(nèi),發(fā)射聲的總功率隨特征速度的增大而增大. 只有四極子聲源的情況下湍流噪聲功率符合8次方定律: