南瓜片微波真空干燥的數學模型
通過南瓜片微波真空干燥的數學模型的建立、模型系數的確定及模型的驗證,表達和預測南瓜片微波真空干燥過程中的水分變化規律。
1、模型的確定
運用表3 中的12 種模型進行擬合求解,并對各模型的擬合度進行分析。利用Matlab 7. 0 軟件對腔體絕對壓力15 kPa,南瓜片厚度6 mm,微波強度12kW/kg 條件下干燥南瓜片的試驗數據進行擬合,各模型的擬合結果如表3 所示。
分析表3 數據可知,Modified Henderson andPabis 模型的R2 最高、SSE 和RMSE 最低,因此該模型的擬合度最好,同時Midilli and Kucuk 模型和Page 模型的擬合度也較好,綜合來看3 種模型的R2均在0. 999 以上,SSE 和RMSE 相差不大,均符合模型擬合的要求,這與本文其它干燥試驗數據的分析結果一致。在保證擬合精度的同時模型參數應盡量少,考慮到Modified Henderson and Pabis 和Midilliand Kucuk 模型參數較多( 分別為6、4 個) ,而Page模型只有2 個,因此選用Page 模型進行預測。
表3 干燥模型的統計參數和系數

2、模型系數的確定
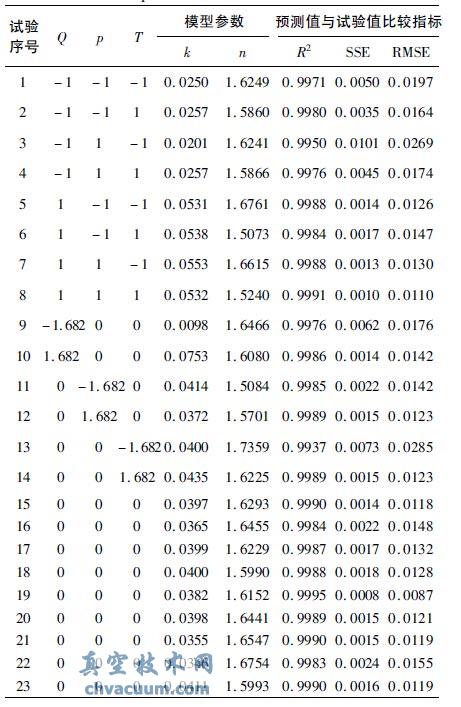
Page 模型中k 代表速率常數,n 代表產品常數,采用響應面法研究微波強度( Q) 、腔體絕對壓力( p)和南瓜片厚度( T) 對k 和n 的影響。該模型與旋轉組合試驗結果擬合得到k 和n 值,并將模型預測值與試驗值進行比較,R2 均在0. 99 以上,SSE 和RMSE 均較小( 見表4) ,說明Page 模型預測值和試驗值匹配度較高。由表4 中k 和n 值可知,干燥條件對k 影響明顯,而對n 影響不大,利用Design Expert7. 0 軟件進行分析,所得模型參數二次方程為:
表4 二次正交旋轉組合試驗的模型參數及模型值與試驗值的比較
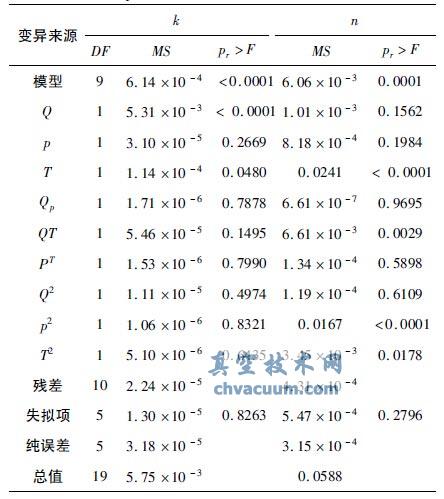
由表5 可知,k 和n 的模型都極顯著( p≤0. 001) 且失擬項不顯著( p > 0. 05) ,說明所得模型很好。從相應的pr < F 可以看出微波強度比腔體絕對壓力和南瓜片厚度對速率常數k 具有更強的影響效果。將差異不顯著項剔除,可得k 和n 的方程為
![]()

表5 響應面法二階模型的方差分析表
3、模型的驗證
為了驗證所選模型的準確度,將不同微波強度下南瓜片微波真空干燥試驗值與預測值進行比較,見圖7。由圖7 可見,Page 模型預測值和試驗值基本一致。因此,可用該模型預測南瓜片微波真空干燥過程中任意時刻的含水率。
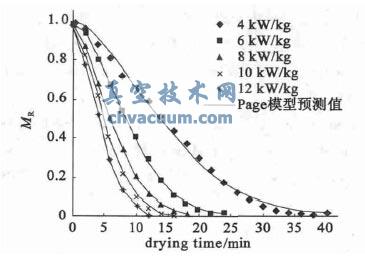
圖7 不同微波強度下的南瓜片微波真空干燥預測值和試驗值比較
與“南瓜片微波真空干燥”相關的文章: