本文建立了真空制冷的數學模型,對絕熱和有熱交換情況下的真空制冷過程進行了理論分析,推導了兩種情況下液體溫度隨時間的變化函數;討論了影響液體溫度變化的各種參數,其中系統壓強p_s 、液體初始溫度T_f0、汽液交界面面積A和外界熱源Q 是影響液體溫度變化的主要因素。在理論計算基礎上,進行了實驗驗證,并對二者進行了分析比較。實驗數據和理論計算結果非常吻合,理論計算能夠很好地預測水溫的變化趨勢。

　　真空制冷的基本原理是利用抽真空降壓而使液體相變蒸發而制冷。在真空制冷的過程中,當外界壓強降低到液體所對應的汽化壓強時,液體就汽化相變,從而帶走大量的蒸發潛熱。當系統與外界絕熱時,沸騰所帶走的蒸發潛熱來自于液體自身的能量,使其冷卻下來,達到制冷降溫的目的。

　　目前真空制冷的研究主要集中在食品冷凍工業,文獻[1]綜述了真空制冷在食品工業中的各種應用,文獻[2]建立了真空冷卻的非穩態數學模型,并利用CFD軟件對多孔食品的真空冷卻進行了數值模擬。文獻[3]綜述了真空冷卻技術在花卉、果蔬和熟肉中的應用研究現狀以及目前真空冷卻技術理論研究的進展。真空制冷具有冷卻速率快、冷卻均勻、蒸發潛熱大等優點,隨著微電子芯片功率不斷增大,真空制冷有望成為冷卻微電子芯片的一種新技術。

　　世界上第一個液體真空制冷模型由Burfoot[4]提出,他認為在氣相和液相之間存在一個濃度梯度,并假設蒸發水的質量流量和質量傳遞系數與水蒸汽的平衡壓力和系統總壓力的壓力差成正比例。Hous-ka[5]、Zitny[6]分別提出了二個不同的真空制冷模型。這些模型是基于氣相和液相的熱力學平衡而得到的。Petera 和Dostal[7]等對液體真空制冷的基本原理、數值模擬作了研究,并對Houska 的模型和Zitny的模型作了比較。

　　盡管Dostal[8]提出的真空制冷模型很好地分析了真空制冷中的傳熱現象,但僅停留在絕熱條件下,且沒有對推導的結論作實驗驗證。本文在Dostal工作的基礎上,建立了真空制冷系統熱傳遞的數學模型,分別在絕熱和有熱交換條件下對真空制冷系統中的液體溫度的變化進行了分析,推導兩種情況下液體溫度隨時間的變化函數,分析影響溫度的各種參數并對理論模型進行實驗驗證,從而為利用真空制冷冷卻微電子芯片提供理論依據。

1、液體真空制冷的數學模型

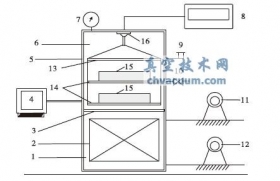
　　真空制冷系統的物理模型如圖1 所示,為了簡化計算,作如下假設[8]:

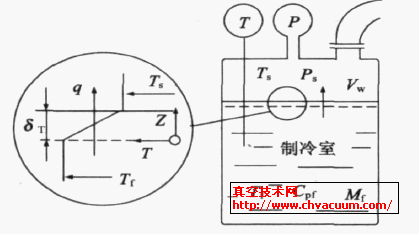
圖1 　真空制冷系統的物理模型圖

　　(1) 在氣相和液相之間存在熱力學平衡,并認為該平衡處于液體表面和其蒸汽之間。

　　(2) 由于在汽液表面間進行的傳熱傳質過程存在著一定的阻力,在靠近氣液界面的一個薄層內,存在著明顯的熱傳遞阻力和質量傳遞阻力。

　　(3) 汽液交界面的溫度Ts由飽和蒸汽壓Ps所對應的平衡值來確定,在液體內部溫度處處相等。

　　(4) 在制冷過程中, 整個系統真空度保持恒定;在液體表面上方空間只有飽和水蒸汽而沒有其它氣體。

　　由圖1 所示,熱傳遞發生在汽液界面的液體薄層內,從等溫液體流向氣液界面的熱流量qz, 寫成一維形式可表示為

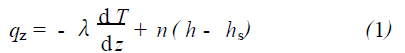
　　式(1) 中T 是液體的溫度,λ是液體的導熱系數, n 是對流質量通量, h 、hs分別是液體內部和氣液界面(移動面) 上的比焓。而焓可以表示為熱容cpf與溫度的積。于是式(1) 可改寫為:

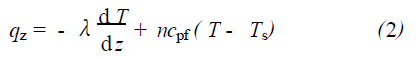
　　式中T、Ts 分別為液體內部溫度和氣液界面(移動面) 的平衡溫度。

　　對式(2) 在z 軸方向作積分, 邊界條件為z = 0時, T = Tf , z =δT 時, T = Ts ,則式(2) 轉化為:

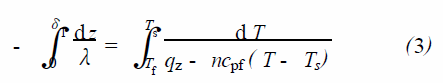
　　忽略在積分區間內參數的變化,熱流量qz 可以表示為:

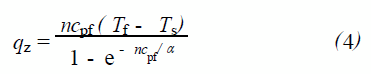
　　上式中α是汽液界面薄膜換熱系數,是由液體薄膜的熱阻δT/λ= 1/α確定的。

　　在式(1) 和(2) 中, 為了確定液體對流質量通量n ,假設在液體中, 對流質量傳遞是主要的傳質過程,分子擴散可忽略。因而質量通量n 可以表示為質量傳遞系數kc 和濃度差Δρf 的乘積。由于蒸發作用,蒸汽的密度遠小于液體的密度,因此我們可以把汽液交界面上的質量通量n 表示為kcρf , 代入到式(4) ,得到:

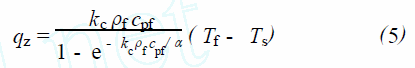
　　式(5)確定了通過氣液交界面的熱流量。從液體中帶走的總的熱流量可以用qz 和氣液交界面面積A的乘積來表示。下面將分兩種條件分別推導液體溫度隨時間變化的關系式:

　　(1) 若系統與外界絕熱,則在汽液交界面下方的控制體積內,液體的非穩態熱平衡可表示為:

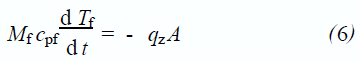
　　假設在制冷過程中, 部分液體蒸發并從液體中帶走蒸發潛熱。由于蒸發的液體質量遠小于固定控制體積內的質量, 因此假設在短時間內Mf 是一個常數。

　　其中Mf ( kg) 為初始質量(包括水和容器的質量) , A為汽液界面面積,將式(5)代入式(6)并積分,考慮液體初始溫度為T _f0 , 得到隨時間變化的液體的溫度T_f :

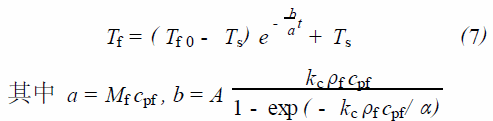
　　(2) 若系統與外界有熱交換,恒定的熱源功率為Q,則在汽液交界面下方的控制體積內,液體的非穩態熱平衡可表示為:

　　將式(5) 代入到式(8) 并積分, 考慮液體的初始溫度為T _f0 ,得到隨時間變化的液體的溫度T_f :

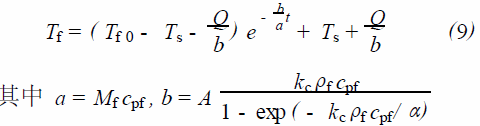
　　從式(7)和(9)可以看到,液體的溫度T_f 與液體初始溫度T _f0 、液體飽和溫度T_s、液體初始質量M_f 、汽液界面面積及液體的熱物性參數有關。液體飽和溫度T_s 與真空系統中所能達到的最低飽和蒸汽壓p_s 有關, 正如假設(3)所述, 汽液交界面的溫度T_s由p_s 所對應的平衡值來確定,即T_s 和p_s 是一一對應的, 它們之間的關系由熱力學決定。p_s 越小, T_s也越小, 則T_f 也越低; 汽液界面面積A 越大, 汽化速率越快,則液體的溫度Tf 越低;而在有熱交換的條件下,液體的溫度Tf 不僅與上述參數有關, 還與外界的換熱量Q有關, Q越大,則T_f反而越高。